7 Hằng Đẳng Thức Đáng Nhớ- Hằng Đẳng Thức Bậc 3

7 hằng đẳng thức đáng nhớ là kiến thức cực kỳ quan trọng trong chương trình toán lớp 8. Kiến thức này được áp dụng phổ biến cả trong phần toán học sau này. 1 phần kiến thức quan trọng trong 7 hằng đẳng thức phải kể đến Hằng đẳng thức bậc 3. 

Với 7 hằng đáng nhớ để các em dễ học, chúng tôi sẽ chia ra làm hằng đẳng thức bậc 2 và Hằng đẳng thức bậc 3.

1. Hằng đẳng thức bậc 2

1.1. Bình phương của một tổng:

Với A, B là giá trị tùy ý, ta luôn có: ( A + B )2 = A2 + 2AB + 2

Chẳng hạn:

a) Tính ( a + 2)2.

b) Viết biểu thức x2+ 6x + 9 dưới dạng bình phương của một tổng.

Lời giải:

a) Ta có: ( a + 2)2= a2+ 2.a.2 + 22 = a22 + 4a + 4.

b) Ta có x2+ 6x + 9 = x2+ 2.x.3 + 32 = ( x + 3 )2.

1.2. Bình phương của một hiệu

Với A, B là giá trị tùy ý, ta có: ( A – B )2 = A2 – 2AB + B2.

Chẳng hạn: (2x-y)2= (2x)2-2.2x.y+y2

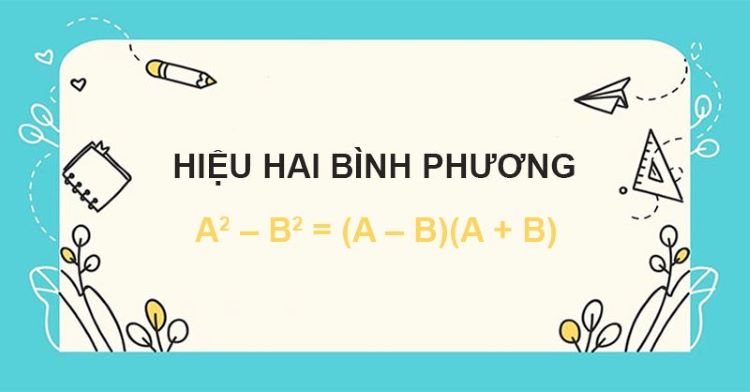
1.3. Hiệu hai bình phương

Với A, B là các giá trị tùy ý, ta có:  A2 – B2 = ( A – B )( A + B ).

Chẳng hạn: 

(2x)2– (3y)2= (2x-3y)(2x+3y)

>> Xem thêm: Công thức cấp số cộng

2. Hằng đẳng thức bậc 3

Đối với hằng đẳng thức bậc 3 cũng được chia ra làm lập phương của 1 tổng, lập phương của 1 hiệu, hiệu hai lập phương, tổng hai lập phương.

2.1. Lập phương của một tổng

Với A, B là các giá trị tùy ý, ta có: ( A + B )3 = A3 + 3A2B + 3AB2 + B3.

Ví dụ: (a+2b)3= a3+6a2b+12ab2+8b3

2.2. Lập phương của một hiệu

Với A, B là các giá trị tùy ý, ta luôn có: ( A – B )3= A3– 3A2B + 3AB2 – B3.

Ví dụ :

a) Tính ( 2x – 2 )2.

b) Viết biểu thức x3– 3x2y + 3xy2– y3 dưới dạng lập phương của một hiệu.

Lời giải:

a) Ta có: ( 2x – 2 )3

= ( 2x )3 – 3.( 2x )2.2 + 3( 2x ).22 – 23

 = 8×3 – 24x2 + 24x – 8

b) Ta có : x3– 3x2y + 3xy2– y3

= ( x )3 – 3.x2.y + 3.x. y2 – y3

= ( x – y )3

>> Tham khảo: Giá bột trét jotun

2.3. Tổng của hai lập phương

Với A, B là các giá trị tùy ý, ta có: A3 + B3 = ( A + B )( A2 – AB + B2 ).

Lưu ý: Người ta hay quy ước A2 – AB + B2 là bình phương thiếu của hiệu A – B.

Ví dụ:

43. a) Tính 33+ 43.
44. b) Viết biểu thức ( x + 2 )( x2- 2x + 4) dưới dạng tổng hai lập phương.

Hướng dẫn:

3. a) Ta có: 33+ 43= ( 3 + 4 )( 32 – 3.4 + 42 ) = 7.13 = 91.
4. b) Ta có: ( x + 2)( x2- x + 4) = x3+ 22= x3 + 2.

2.4. Hiệu hai lập phương

Với A, B là các giá trị tùy ý, ta có: A3– B3 = ( A – B )( A2+ AB + B2 ).

Chú ý: Ta quy ước A2 + AB + B2 là bình phương thiếu của tổng A + B.

Ví dụ:

43. a) Tính 63– 43.
44. b) Viết biểu thức ( x – 4y )( x2+ 4xy + 16y2) dưới dạng hiệu hai lập phương

Lời giải

6. a) Ta có: 63– 43= ( 6 – 4 )( 62 + 6.4 + 42 ) = 2.76 = 152.
7. b) Ta có : ( x – 4y )( x2+ 4xy + 16y2) = ( x )3 – ( 4y )3 = x3 – 64y3.

 

3. Các hằng đẳng thức mở rộng

Ngoài 7 hằng đẳng thức đáng nhớ trên, còn một số hằng đẳng thức đáng nhớ với hàm mở rộng bậc 2 và bậc 3. Hằng đẳng thức tổng quát có dạng như sau:

Hằng đẳng thức mở rộng bậc hai

(a + b + c)2= a2 + b2 + c2 + 2ab + 2ac + 2bc

(a + b – c)2 = a2 + b2 + c2 + 2ab – 2ac – 2bc

(a – b – c)2 = a2 + b2 + c2 – 2ab – 2ac + 2bc

 

Hằng đẳng thức mở rộng bậc ba

a3 + b3 = (a + b)3 – 3ab(a + b)

a3 – b3 = (a – b)3 + 3ab(a – b)

(a + b + c)3 = a3 + b3 + c3 + 3(a + b)(a + c)(b + c)

a3 + b3 + c3 − 3abc = (a + b + c)(a2 + b2 + c2 − ab − bc − ca)

(a – b)3 + (b – c)3 + (c – a)3 = 3(a – b)(b – c)(c – a)

(a + b)(b + c)(c + a) – 8abc = a(b – c)2 + b(c – a)2 + c(a – b)2

(a + b)(b + c)(c + a) = (a + b + c)(ab + bc + ca) − abc

(a + b)(b + c)(c + a) – 8abc = a(b – c)2 + b(c – a)2 + c(a – b)2

(a + b)(b + c)(c + a) = (a + b + c)(ab + bc + ca) − abc

Hằng đẳng thức có dạng tổng quát như sau:

an + bn = (a + b)(an-1 − an-2b + an-3b2 − an-4b3 + … + a2bn-3 − a.bn-2 + bn-1) (1), với n là số lẻ thuộc tập N

an – bn = (a – b)(an-1 + an-2b + an-3b2 + … + a2bn-3 + a.bn-2 + bn-1)

4. Cách ghi nhớ các hằng đẳng thức bậc 3, đẳng thức bậc 2

Hiểu bản chất: Để ghi nhớ, bạn cần hiểu rõ ý nghĩa và cách hoạt động của các hằng đẳng thức. Nếu bạn hiểu tại sao chúng được hoạt động như vậy bạn sẽ ghi nhớ chúng dễ hơn.

Lên lịch ôn tập: Xây dựng kế hoạch ôn tập thường xuyên sẽ giúp bạn ghi nhớ kiến thức một cách hiệu quả.

Sử dụng phương pháp nhớ: Có thể áp dụng các cách ghi nhớ khác nhau như viết chúng ra, lập các mẫu thức đẳng thức hay tạo những câu nhớ ngắn về chúng.

Giải các bài tập thực hành: Làm nhiều bài tập sẽ giúp bạn làm quen với cách áp dụng chúng trong các tình huống khác nhau.

Giảng dạy cho người khác: Một cách có thể ghi nhớ dễ dàng đó là cố gắng giảng dạy lại cho người khác. Khi bạn giải thích cho người khác, bạn cần phải hiểu sâu hơn và điều này giúp bạn củng cố kiến thức.

Học tập cùng nhóm: Học cùng nhóm cũng là cách giúp bạn chia sẻ kiến thức và học từ nhau. Mỗi người có thể có góc nhìn và cách nhớ riêng, điều này sẽ giúp bạn ghi nhớ dễ dàng.