Công Thức Cấp Số Cộng Hướng Dẫn Chi Tiết Và Bài Tập Ví Dụ

Cấp số cộng là một trong những kiến thức cơ bản nhưng cực kỳ quan trọng trong chương trình toán học từ trung học cơ sở đến phổ thông. Việc nắm vững công thức cấp số cộng giúp học sinh giải quyết các bài toán về dãy số, tính tổng, cũng như áp dụng vào các bài toán thực tế một cách nhanh chóng. Bài viết này sẽ giải thích chi tiết, đưa ra ví dụ minh họa, phân tích bài tập nâng cao, đồng thời hướng dẫn mẹo học hiệu quả để ghi nhớ công thức lâu dài.

Cấp số cộng là gì?

Khái niệm cơ bản về cấp số cộng

Cấp số cộng là một dãy số mà hiệu giữa hai số liên tiếp là hằng số. Nếu dãy số là a1, a2, a3, …, an thì:

a2 – a1 = a3 – a2 = … = an – a(n-1) = d

Trong đó d gọi là công sai. Dãy số có tính chất này giúp người học dễ dàng dự đoán các số hạng tiếp theo và tính tổng các số hạng trong dãy.

Ví dụ: Dãy số 2, 5, 8, 11, 14,… là cấp số cộng với công sai d = 3. Hiểu được khái niệm này sẽ giúp bạn áp dụng dễ dàng công thức cấp số cộng vào các bài toán khác nhau.

Các ký hiệu thường dùng

Khi làm việc với cấp số cộng, một số ký hiệu phổ biến mà bạn cần nắm:

a1: số hạng đầu tiên

an: số hạng thứ n

d: công sai

Sn: tổng n số hạng đầu

Những ký hiệu này sẽ giúp bạn dễ dàng sử dụng các công thức để giải quyết các bài toán tính số hạng, tính tổng hay tìm công sai trong cấp số cộng.

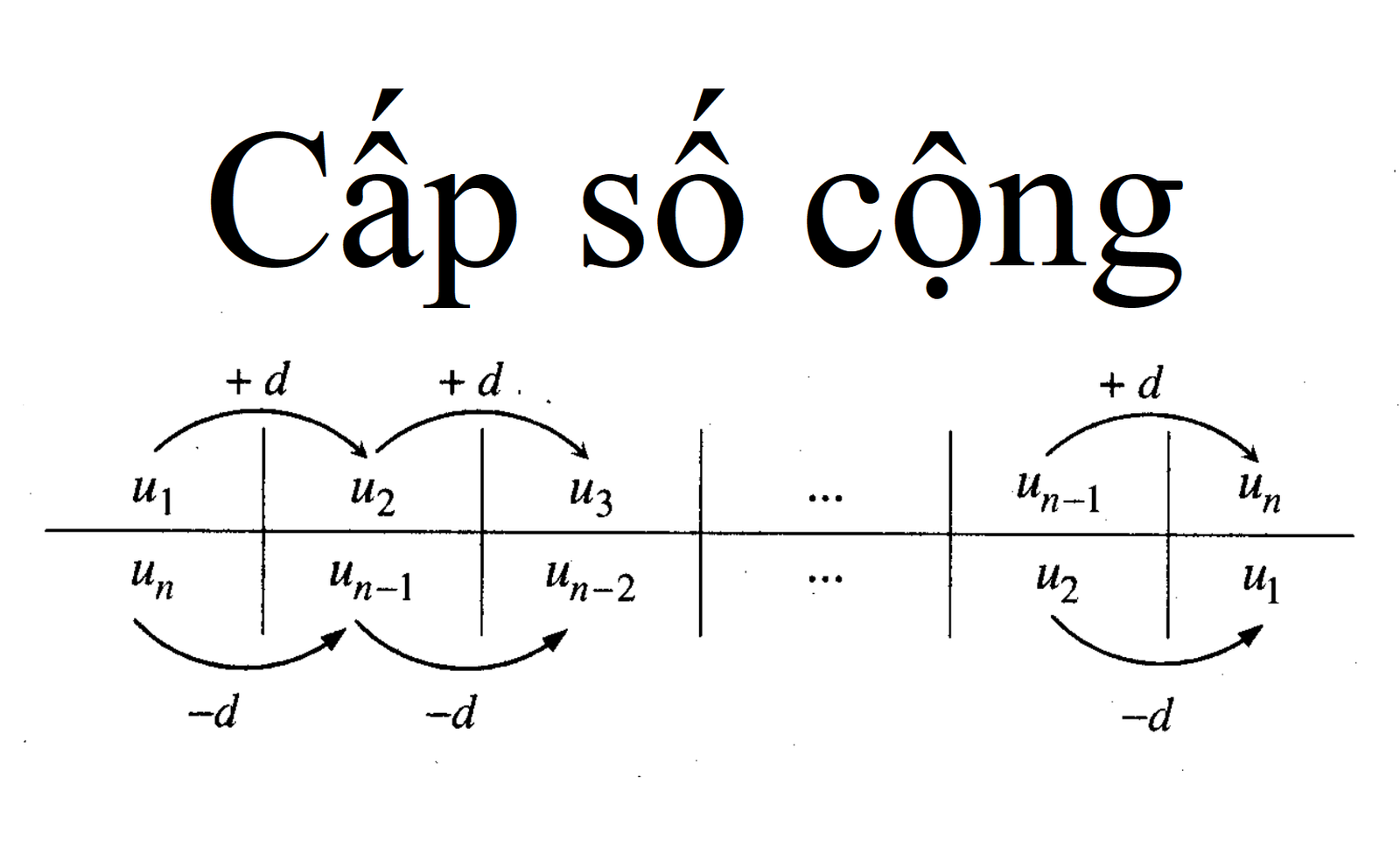
Công thức cấp số cộng

Công thức tính số hạng thứ n

Công thức cơ bản để tính số hạng thứ n trong cấp số cộng là:

a_n = a_1 + (n – 1) * d

Trong đó:

a1: số hạng đầu

d: công sai

n: vị trí số hạng cần tính

Ví dụ: Cho dãy số 3, 7, 11, 15,… Tính số hạng thứ 10:

a_10 = 3 + (10 – 1) * 4 = 3 + 36 = 39

Vậy số hạng thứ 10 là 39.

Công thức tính tổng n số hạng đầu

Công thức tổng quát để tính tổng n số hạng đầu của cấp số cộng là:

S_n = n/2 * (a_1 + a_n)

Hoặc có thể viết theo công thức thay thế:

S_n = /2 * [2 * a_1 + (n – 1) * d]

Trong đó:

Sn: tổng n số hạng đầu

a1: số hạng đầu

an: số hạng thứ n

d: công sai

Ví dụ: Cho dãy số 2, 5, 8, 11,… Tính tổng 20 số hạng đầu.

a_20 = 2 + (20-1)*3 = 59

S_20 = 20/2 * (2 + 59) = 10 * 61 = 610

Vậy tổng 20 số hạng đầu là 610.

Công thức liên quan khác

Ngoài các công thức cơ bản, còn một số công thức mở rộng thường dùng:

Tìm công sai d:

d = (a_n – a_1) / (n – 1)

Tìm số hạng giữa hai số hạng bất kỳ:

a_m = a_k + (m – k) * d

 

Các công thức này hữu ích trong các bài toán nâng cao hoặc áp dụng thực tế, đặc biệt khi bạn biết hai số hạng bất kỳ và muốn tính số hạng còn lại.

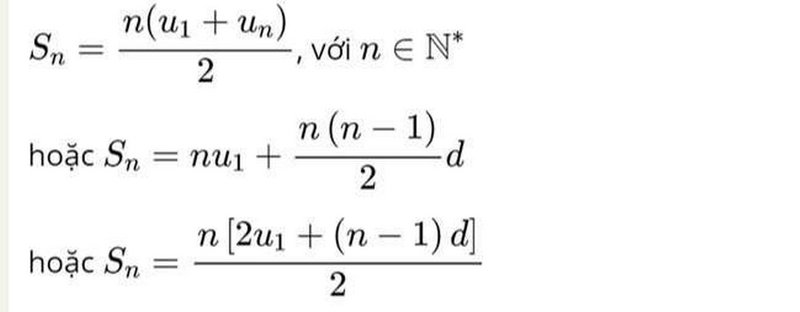
Ví dụ minh họa công thức cấp số cộng

Ví dụ tính số hạng thứ n

Bài toán: Cho dãy số 7, 10, 13, 16,… Tìm số hạng thứ 15:

a_15 = 7 + (15 – 1) * 3 = 7 + 42 = 49

Vậy số hạng thứ 15 là 49.

Ví dụ tính tổng n số hạng đầu

Bài toán: Tính tổng 30 số hạng đầu của dãy số trên:

a_30 = 7 + (30 – 1)*3 = 94

S_30 = 30/2 * (7 + 94) = 15 * 101 = 1515

Vậy tổng 30 số hạng đầu là 1515.

Bài toán nâng cao kết hợp công thức

Bài toán: Cho dãy số 4, 7, 10,… Tìm n để tổng n số hạng đầu là 550:

S_n = n/2 * [2*4 + (n-1)*3] = 550

n/2 * (8 + 3n – 3) = 550

n*(3n + 5)/2 = 550

3n^2 + 5n – 1100 = 0

Giải phương trình bậc hai: n = 18

Vậy tổng 550 đạt được với 18 số hạng đầu.

Mẹo học và ghi nhớ công thức cấp số cộng hiệu quả

Sử dụng sơ đồ hoặc bảng biểu

Vẽ sơ đồ hoặc bảng biểu giúp bạn dễ quan sát số hạng, công sai và tổng số hạng. Ví dụ:

n	a_n	S_n
1	a1	a1
2	a1 + d	a1 + a2
3	a1 + 2d	a1 + a2 + a3

Cách này giúp học sinh dễ ghi nhớ công thức và hình dung mối liên hệ giữa các số hạng.

Thường xuyên luyện tập bài tập

Chia bài tập theo mức độ:

Cơ bản: Tính số hạng thứ n, tổng n số hạng đầu

Nâng cao: Tìm số hạng, công sai, giải phương trình liên quan đến tổng

Ứng dụng thực tế: Lãi suất, dãy số tiến hành đều, dự đoán số hạng tiếp theo

Việc luyện tập thường xuyên giúp ghi nhớ công thức và tăng tốc độ giải toán.

Ứng dụng vào thực tế

Cấp số cộng không chỉ xuất hiện trong toán học, mà còn áp dụng vào:

Tính lãi suất ngân hàng: Lãi suất tăng đều hàng tháng có thể mô hình hóa bằng cấp số cộng

Dự đoán số hạng tiếp theo trong dãy số: Ví dụ, số lượng sản phẩm tăng đều theo ngày

Giải quyết bài toán tiến trình đều: Như tính số bước, khoảng cách hoặc thời gian

Cấp số cộng là kiến thức quan trọng trong toán học, từ lý thuyết đến ứng dụng thực tế.

Công thức số hạng thứ n: a_n = a_1 + (n – 1) * d

Công thức tổng n số hạng đầu: S_n = n/2 * (a_1 + a_n) hoặc S_n = n/2 * [2 * a_1 + (n – 1) * d]

Nắm vững công thức cấp số cộng, kết hợp ví dụ minh họa và luyện tập thường xuyên sẽ giúp học sinh giải quyết các bài toán từ cơ bản đến nâng cao, đồng thời áp dụng vào thực tế một cách hiệu quả.