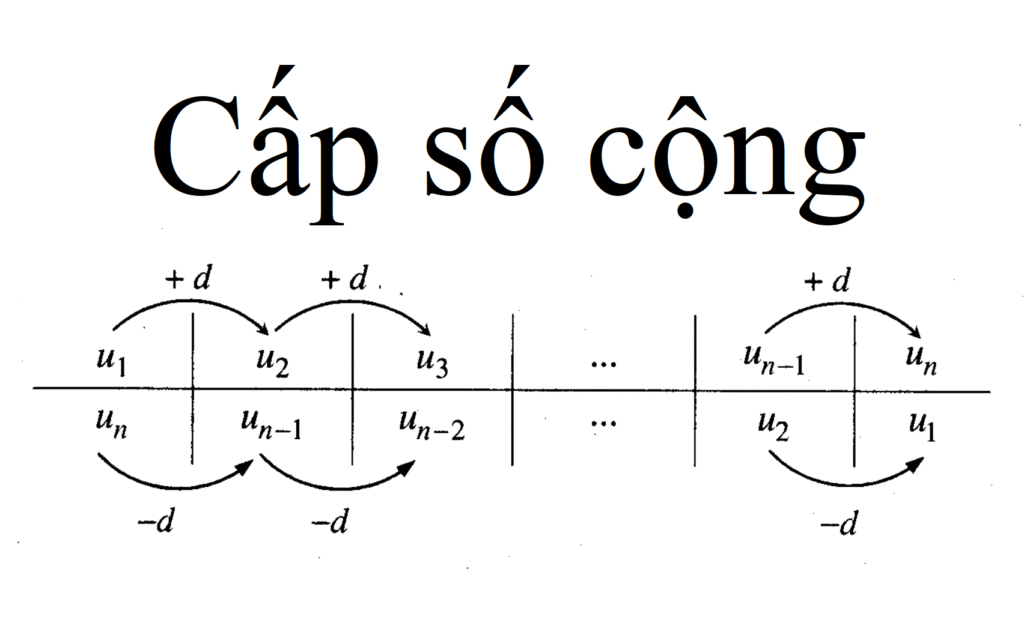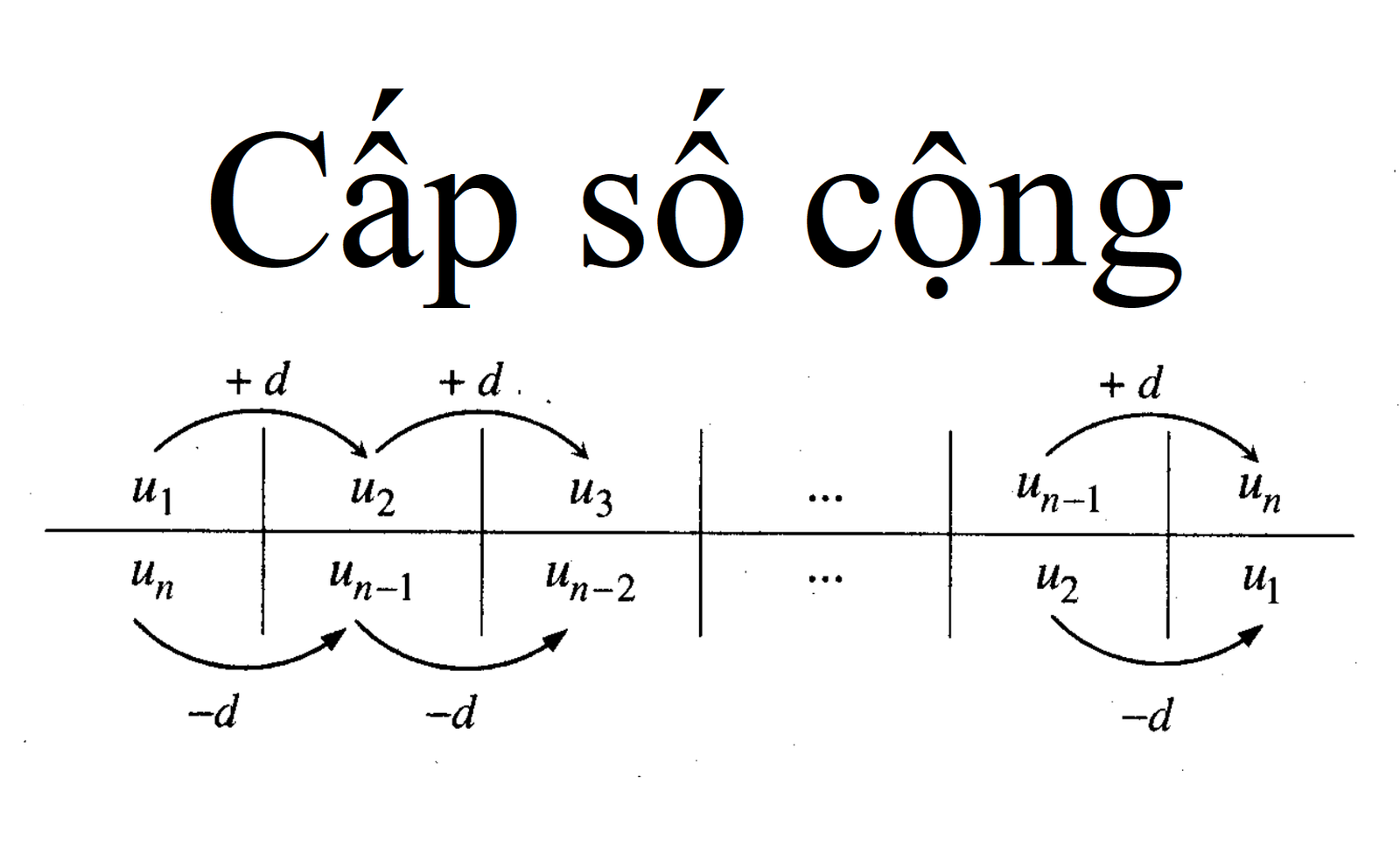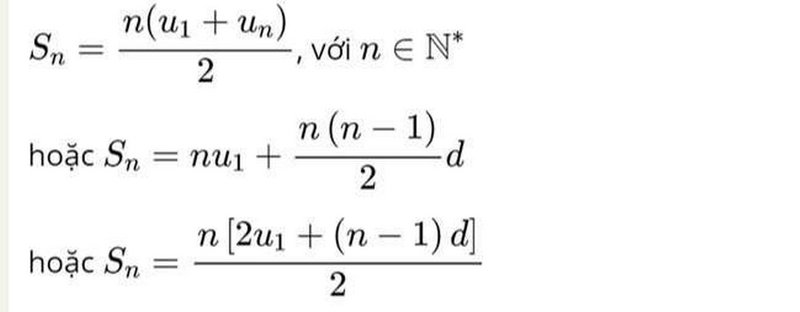Công thức cấp số cộng: Kiến thức nền tảng và ứng dụng toàn diện

Công thức cấp số cộng là công cụ quan trọng giúp giải nhanh các bài toán dãy số và tính tổng. Khám phá chi tiết công thức, ví dụ minh họa, lỗi thường gặp và ứng dụng thực tế.

Cấp số cộng là gì?

Trước khi tìm hiểu chi tiết về công thức cho cấp số cộng, cần nắm vững khái niệm cơ bản. Cấp số cộng là một dãy số có đặc điểm nổi bật: hiệu số giữa hai số hạng liên tiếp luôn bằng một hằng số cố định, gọi là công sai.

Dãy số a₁, a₂, a₃, …, aₙ là một cấp số cộng khi và chỉ khi:

a₂ – a₁ = a₃ – a₂ = … = aₙ – aₙ₋₁ = d

Trong đó:

a₁: số hạng đầu tiên

d: công sai (common difference)

n: số thứ tự của số hạng

Ví dụ: Dãy 4, 7, 10, 13, … là một cấp số cộng với số hạng đầu a₁ = 4 và công sai d = 3.

Ý nghĩa của khái niệm cấp số cộng

Cấp số cộng là dạng đặc biệt của dãy số có quy luật đơn giản nhưng xuất hiện rộng rãi trong toán học và đời sống. Việc hiểu rõ cấp số cộng là nền tảng để học sinh dễ dàng tiếp cận các kiến thức cao hơn như cấp số nhân, chuỗi số, dãy vô hạn.

Minh họa dãy số cấp số cộng tăng đều

Các công thức cấp số cộng quan trọng

Có hai công thức về cấp số cộng thường gặp: công thức số hạng tổng quát và công thức tính tổng n số hạng đầu.

Công thức số hạng tổng quát

aₙ = a₁ + (n – 1)d

Công thức này cho phép tìm số hạng thứ n khi biết số hạng đầu và công sai. Đây là công thức cơ bản nhất, giúp xác định bất kỳ số hạng nào trong dãy mà không cần liệt kê từng bước.

Công thức tính tổng n số hạng đầu

Có hai cách viết:

Sₙ = n(a₁ + aₙ) / 2
hoặc
Sₙ = n[2a₁ + (n – 1)d] / 2

Trong đó Sₙ là tổng của n số hạng đầu tiên.

Cách ghi nhớ nhanh

Có thể hiểu công thức tổng như sau: “Số lượng số hạng nhân với giá trị trung bình của số hạng đầu và số hạng cuối.” Đây là cách suy luận trực quan, giúp học sinh ghi nhớ dễ dàng.

 Sơ đồ tính tổng bằng công thức về cấp số cộng

Ví dụ minh họa áp dụng công thức cho cấp số cộng

Để hiểu sâu hơn, hãy xét một số bài toán cụ thể.

Ví dụ 1: Cho cấp số cộng 2, 6, 10, … Hãy tìm số hạng thứ 15.

a₁ = 2, d = 4, n = 15

a₁₅ = 2 + (15 – 1) x 4 = 2 + 56 = 58

Ví dụ 2: Tính tổng 30 số hạng đầu của cấp số cộng 5, 9, 13, …

a₁ = 5, d = 4, n = 30

a₃₀ = 5 + (30 – 1) x 4 = 5 + 116 = 121

S₃₀ = 30(5 + 121) / 2 = 30 x 126 / 2 = 1890

Ví dụ 3: Một cấp số cộng có a₁ = 7, d = 5. Hãy tính tổng 50 số hạng đầu.

S₅₀ = 50[2 x 7 + (50 – 1) x 5] / 2

S₅₀ = 50(14 + 245) / 2 = 50 x 259 / 2 = 6475

Phân tích ví dụ

Qua các ví dụ, có thể thấy công thức cho cấp số cộng giúp tiết kiệm đáng kể thời gian tính toán. Thay vì cộng lần lượt, chỉ cần áp dụng công thức là có kết quả nhanh chóng.

Ứng dụng công thức của cấp số cộng trong thực tế tài chính

Các dạng bài toán thường gặp với công thức về cấp số cộng

Khi học về cấp số cộng, học sinh sẽ gặp nhiều dạng toán khác nhau, tất cả đều liên quan đến công thức.

Dạng tìm số hạng tổng quát

Bài toán thường cho số hạng đầu và công sai, yêu cầu tìm số hạng thứ n. Đây là dạng cơ bản nhất, chỉ cần áp dụng công thức trực tiếp.

Dạng tính tổng n số hạng đầu

Dạng này thường xuất hiện trong đề thi. Bài toán có thể yêu cầu tính tổng 10, 20 hoặc 100 số hạng đầu tiên. Công thức tính tổng giúp giải nhanh thay vì cộng dồn.

Dạng ngược: tìm số hạng đầu hoặc công sai

Có những bài toán cho biết số hạng thứ n và số hạng đầu, yêu cầu tìm công sai d. Ngược lại, đôi khi đề bài cho tổng và yêu cầu tìm d hoặc n. Khi đó, cần linh hoạt biến đổi công thức.

Dạng ứng dụng thực tế

Bài toán thực tế có thể là: “Một rạp chiếu phim có hàng ghế đầu tiên 15 ghế, mỗi hàng sau thêm 2 ghế. Hỏi 20 hàng có bao nhiêu ghế?” Đây chính là ứng dụng trực tiếp của công thức cấp số cộng.

Ứng dụng công thức về cấp số cộng trong thực tiễn

Không chỉ gói gọn trong toán học, công thức cấp số cộng còn hiện diện trong đời sống hàng ngày.

Trong xây dựng, khi thiết kế bậc thang có độ cao bằng nhau, tính tổng chiều cao hoặc tổng chiều dài cầu thang chính là một ứng dụng.

Trong tài chính, khi tiết kiệm đều đặn mỗi tháng một khoản tiền cố định, tổng số tiền sau n tháng chính là tổng cấp số cộng.

Trong thể thao, khi tính tổng quãng đường chạy với vận tốc tăng đều mỗi vòng, công thức về cấp số cộng cũng phát huy hiệu quả.

Ý nghĩa trong lập trình và khoa học dữ liệu

Trong các ngôn ngữ lập trình, công thức này được sử dụng để tính toán vòng lặp, mô phỏng dữ liệu hoặc xử lý các bài toán dãy số có quy luật. Điều đó cho thấy cấp số cộng không chỉ là bài toán trên giấy, mà còn là công cụ thực tiễn trong công nghệ hiện đại.

Bài tập vận dụng công thức về cấp số cộng

Để rèn luyện, bạn có thể thử giải một số bài tập sau.

Bài 1: Cho cấp số cộng có a₁ = 4, d = 6. Hãy tính số hạng thứ 25.
Bài 2: Tính tổng 15 số hạng đầu tiên của cấp số cộng 1, 4, 7, …
Bài 3: Một cấp số cộng có a₁ = 3, a₁₀ = 30. Hãy tìm công sai d và tính tổng 10 số hạng đầu.
Bài 4: Một người tiết kiệm 2 triệu tháng đầu, các tháng sau mỗi tháng tăng thêm 500 nghìn. Hỏi sau 12 tháng, tổng số tiền tiết kiệm được là bao nhiêu?

Khi luyện tập, bạn sẽ nhận ra sự tiện lợi của việc áp dụng công thức về cấp số cộng thay vì cộng dồn từng số.

Công thức cấp số cộng là một trong những công cụ toán học nền tảng, vừa đơn giản vừa có giá trị ứng dụng cao. Với công thức số hạng tổng quát và công thức tính tổng, học sinh có thể giải quyết nhanh chóng nhiều dạng bài toán khác nhau. Việc nắm vững và rèn luyện thường xuyên không chỉ giúp học tốt môn Toán mà còn phát triển tư duy logic để áp dụng trong thực tiễn đời sống.