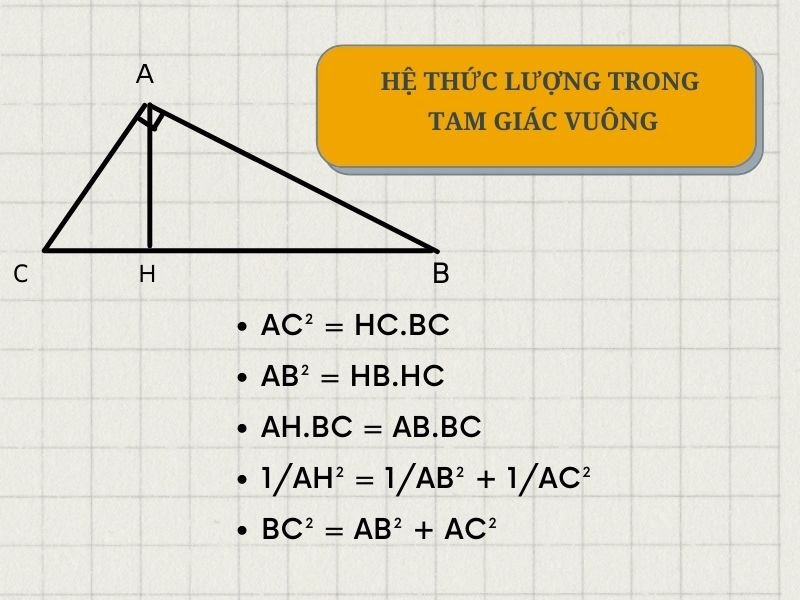
Giải Thích Hệ Thức Lượng Trong Tam Giác Vuông: Công Thức Và Ứng Dụng

Hệ thức lượng trong tam giác vuông là một phần quan trọng trong toán học, giúp xác định mối quan hệ giữa các cạnh và góc của tam giác vuông. Việc nắm vững hệ thức lượng không chỉ hỗ trợ giải bài tập mà còn áp dụng vào nhiều lĩnh vực thực tế. Cùng khám phá chi tiết qua bài viết dưới đây.

Hệ thức lượng trong tam giác vuông

1.Hệ thức lượng trong tam giác vuông là gì?

Hệ thức lượng trong tam giác vuông là tập hợp các công thức toán học dùng để xác định mối quan hệ giữa các cạnh và các góc trong một tam giác vuông. Đây là nền tảng quan trọng trong hình học và lượng giác, giúp tính toán độ dài các cạnh, đo góc, cũng như áp dụng trong các bài toán thực tế như xây dựng, định vị hay kỹ thuật.

Các hệ thức lượng cơ bản thường dựa trên định lý Pythagore và các hàm lượng giác (sin, cos, tan, cot) như sau:

• Định lý Pythagore:
  a² + b² = c²
  Trong đó:
  c là cạnh huyền
  a, b là hai cạnh góc vuông
• Hàm lượng giác cơ bản:
  sin A = cạnh đối / cạnh huyền
  cos A = cạnh kề / cạnh huyền
  tan A = cạnh đối / cạnh kề

Nhờ những hệ thức này, bạn có thể dễ dàng tính toán các cạnh hoặc góc còn thiếu trong tam giác vuông mà không cần đo trực tiếp.

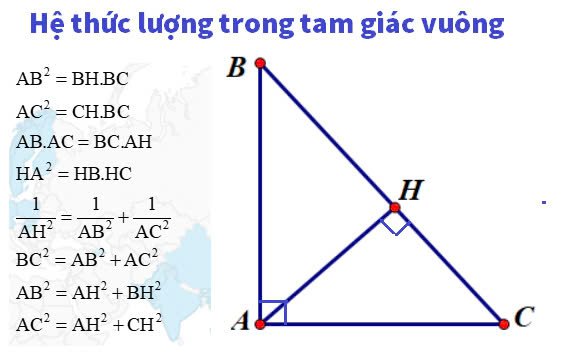
2.Tại sao hệ thức lượng tam giác vuông lại quan trọng trong toán học?

Hệ thức lượng tam giác vuông có vai trò vô cùng quan trọng trong toán học bởi nó là cơ sở để giải quyết các bài toán về hình học, lượng giác và các ứng dụng thực tiễn. Nhờ hệ thức lượng, chúng ta có thể xác định các cạnh và góc trong tam giác vuông một cách chính xác mà không cần đo trực tiếp.

Một số lý do khiến hệ thức lượng quan trọng:

• Công cụ tính toán cơ bản: Dựa trên định lý Pythagore và các hàm lượng giác, hệ thức lượng giúp giải quyết các bài toán liên quan đến độ dài cạnh và số đo góc.
• Áp dụng rộng rãi trong thực tế: Hệ thức lượng được sử dụng trong xây dựng, định vị, kỹ thuật, vật lý, đồ họa máy tính và nhiều lĩnh vực khoa học khác.
• Nền tảng của lượng giác: Hệ thức lượng tam giác vuông là cơ sở để phát triển các khái niệm lượng giác nâng cao như sin, cos, tan trong tam giác bất kỳ.
• Hỗ trợ tư duy logic: Việc áp dụng hệ thức lượng giúp rèn luyện kỹ năng suy luận, phân tích và giải quyết vấn đề trong toán học.

Nhờ những lý do trên, hệ thức lượng tam giác vuông được coi là một phần quan trọng và không thể thiếu trong chương trình toán học cơ bản và nâng cao.

3.Có những công thức hệ thức lượng nào trong tam giác vuông?

Trong tam giác vuông, hệ thức lượng được xây dựng dựa trên định lý Pythagore và các hàm lượng giác cơ bản (sin, cos, tan, cot). Dưới đây là các công thức phổ biến:

• Định lý Pythagore:
  a² + b² = c²
  Trong đó:
  c là cạnh huyền
  a, b là hai cạnh góc vuông
• Hàm lượng giác cơ bản:
  sin A = cạnh đối / cạnh huyền
  cos A = cạnh kề / cạnh huyền
  tan A = cạnh đối / cạnh kề
  cot A = cạnh kề / cạnh đối
• Công thức suy rộng từ hàm lượng giác:
  cạnh đối = cạnh huyền × sin góc
  cạnh kề = cạnh huyền × cos góc
  cạnh đối = cạnh kề × tan góc
• Công thức liên hệ giữa các góc:
  tan A = 1 / tan B
  sin² A + cos² A = 1

Nhờ những công thức này, bạn có thể dễ dàng tính toán các cạnh hoặc góc còn thiếu trong tam giác vuông và áp dụng vào nhiều bài toán thực tế.

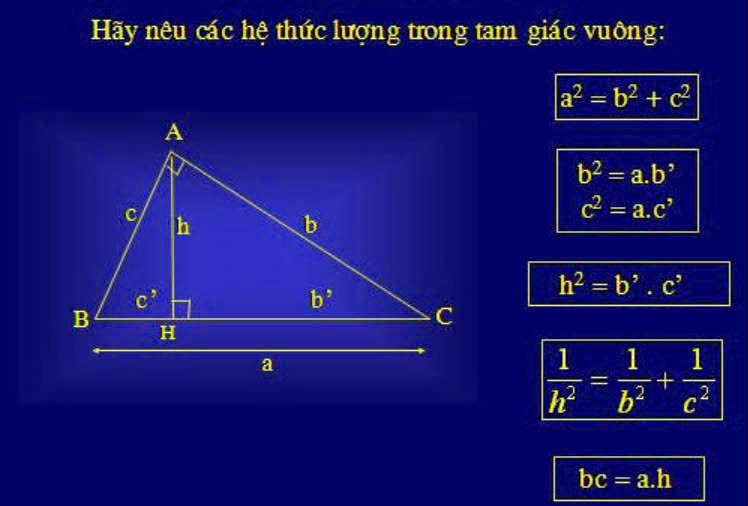
4.Làm thế nào để áp dụng hệ thức lượng tam giác vuông vào giải bài tập?

Áp dụng hệ thức lượng tam giác vuông vào giải bài tập yêu cầu bạn nắm vững các công thức cơ bản và biết cách xác định cạnh hoặc góc cần tính. Dưới đây là hướng dẫn cơ bản:

• Bước 1: Xác định các yếu tố đã biết và cần tìm
  Ghi chú các cạnh, góc đã biết trong tam giác vuông và xác định thông tin cần tìm.
• Bước 2: Chọn công thức phù hợp
  • Nếu biết hai cạnh và cần tính cạnh còn lại → sử dụng định lý Pythagore: a² + b² = c²
  • Nếu biết một cạnh và một góc (không phải góc vuông) → sử dụng hàm lượng giác cơ bản: sin, cos, tan, cot
• Bước 3: Thiết lập phương trình và giải
  Thay số vào công thức tương ứng và giải phương trình để tìm cạnh hoặc góc còn thiếu.
• Bước 4: Kiểm tra kết quả
  Đảm bảo tổng các góc bằng 90° (trong tam giác vuông) và các cạnh thỏa mãn định lý Pythagore.
• Bước 5: Áp dụng thực tế (nếu có)
  Trong các bài toán ứng dụng thực tế, như tính chiều cao, khoảng cách hoặc góc nghiêng, hệ thức lượng giúp tính toán nhanh chóng và chính xác.

Ví dụ bài tập áp dụng hệ thức lượng tam giác vuông:

Bài tập 1:
Tam giác vuông ABC, góc C = 90°, cạnh AC = 3 cm, BC = 4 cm. Tính cạnh AB.

Giải: AB² = AC² + BC² = 3² + 4² = 9 + 16 = 25 → AB = 5 cm

Bài tập 2:
Tam giác vuông ABC, góc C = 90°, cạnh AC = 5 cm, góc A = 30°. Tính cạnh BC.

Giải: sin A = đối/huyền → sin 30° = BC / AB
AB = AC / cos A = 5 / cos 30° ≈ 5,77 cm
BC = AB × sin 30° ≈ 5,77 × 0,5 ≈ 2,885 cm

Bài tập 3 (ứng dụng thực tế):
Một chiếc thang dài 10 m dựa vào tường, chân thang cách tường 6 m. Tính chiều cao mà thang chạm vào tường.

Giải: Đây là tam giác vuông, chiều cao = √(10² – 6²) = √(100 – 36) = √64 = 8 m

Nhờ các bài tập trên, học sinh có thể hiểu cách áp dụng hệ thức lượng vào cả bài toán hình học cơ bản và bài toán thực tế.

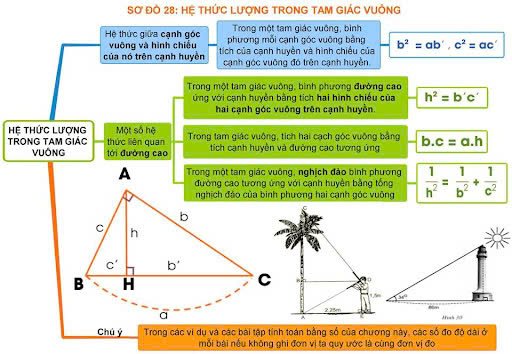
5.Ví dụ thực tế về việc sử dụng hệ thức lượng trong tam giác vuông là gì?

Hệ thức lượng tam giác vuông không chỉ quan trọng trong toán học lý thuyết mà còn được áp dụng rộng rãi trong đời sống thực tế và các ngành kỹ thuật. Dưới đây là một số ví dụ minh họa:

• Xây dựng và kiến trúc:Khi thiết kế mái nhà, cầu thang hay dốc nghiêng, kỹ sư sử dụng định lý Pythagore và các hàm lượng giác để tính toán chiều cao, độ dài cạnh và góc nghiêng chính xác.
• Định vị và đo đạc:Trong địa lý và bản đồ, hệ thức lượng giúp xác định khoảng cách từ điểm quan sát đến vật thể, hoặc đo chiều cao núi, cây cối mà không cần tiếp cận trực tiếp.
• Kỹ thuật và vật lý:Trong cơ khí, thiết kế máy móc hoặc đo lường lực tác động theo phương nghiêng, hệ thức lượng giúp tính toán các thành phần lực, chiều dài cần thiết cho các bộ phận máy.
• Hàng không và hàng hải:Phi công và thủy thủ sử dụng hệ thức lượng  tam giác vuông để tính góc bay, quãng đường bay hoặc khoảng cách từ tàu đến bờ dựa trên các dữ liệu đo được.
• Cuộc sống hàng ngày:Ví dụ khi đặt thang dựa vào tường, muốn biết chiều cao chạm tường hoặc khoảng cách chân thang từ tường, bạn có thể áp dụng định lý Pythagore rất dễ dàng.

Nhờ các ứng dụng này, hệ thức lượng tam giác vuông trở thành công cụ quan trọng và thiết thực trong cả học tập lẫn đời sống hàng ngày.

Trên đây chúng tôi đã cùng bạn tìm hiểu chi tiết về hệ thức lượng trong tam giác vuông, từ các công thức cơ bản, cách áp dụng vào giải bài tập, đến những ví dụ thực tế trong đời sống và kỹ thuật. Việc nắm vững hệ thức lượng không chỉ giúp giải quyết các bài toán hình học mà còn mở rộng hiểu biết về ứng dụng của toán học trong thực tế.

Hy vọng bài viết đã mang đến cho bạn những thông tin bổ ích, giúp dễ dàng áp dụng hệ thức lượng tam giác vuông vào học tập và công việc hàng ngày.