Hằng Đẳng Thức Bậc 3 Giải Thích Chi Tiết, Ví Dụ Minh Họa

Hằng đẳng thức bậc 3 là một trong những kiến thức quan trọng trong chương trình toán học phổ thông, đặc biệt là lớp 9. Nắm vững các công thức và cách áp dụng hằng đẳng thức bậc 3 giúp học sinh rút gọn biểu thức phức tạp, giải phương trình bậc 3 nhanh chóng, và nâng cao khả năng tư duy đại số. Trong bài viết này, chúng ta sẽ tìm hiểu khái niệm, các công thức cơ bản, ví dụ minh họa, mẹo học và ứng dụng thực tế của hằng đẳng thức 

Cấp số và hằng đẳng thức là những kiến thức nền tảng giúp học sinh dễ dàng tiếp cận các dạng toán nâng cao. Nếu hằng đẳng thức bậc 2 được học nhiều trong lớp 8 và 9, thì hằng đẳng thức bậc 3 mở rộng khả năng giải quyết các bài toán rút gọn biểu thức và phân tích đa thức phức tạp.

Hằng đẳng thức bậc 3 là gì?

Hằng đẳng thức bậc 3 là các công thức liên quan đến lập phương của một tổng, hiệu hoặc hiệu/tổng lập phương của hai số, cho phép rút gọn biểu thức hoặc phân tích đa thức thành nhân tử. Hằng đẳng thức là bước nâng cao hơn của hằng đẳng thức bậc 2 và thường xuất hiện trong các bài toán giải phương trình, rút gọn biểu thức và luyện thi học sinh giỏi.

Ví dụ minh họa khái niệm: Dãy công thức cơ bản về hằng đẳng thức

(x + y)³ = x³ + y³ + 3xy(x + y)

(x – y)³ = x³ – y³ – 3xy(x – y)

Nhờ những công thức này, các bài toán liên quan đến lập phương hai số trở nên đơn giản và dễ giải quyết hơn.

Các dạng hằng đẳng thức bậc 3 cơ bản

Lập phương của một tổng hoặc hiệu

Công thức lập phương của tổng hai số:

(x + y)³ = x³ + y³ + 3xy(x + y)

Công thức lập phương của hiệu hai số:

(x – y)³ = x³ – y³ – 3xy(x – y)

Ví dụ minh họa:

Tính (2 + 5)³ theo công thức hằng đẳng thức:

(2 + 5)³ = 2³ + 5³ + 3*2*5*(2 + 5) = 8 + 125 + 30*7 = 133 + 210 = 343

 

Vậy (2 + 5)³ = 343, đúng bằng cách tính trực tiếp.

Hiệu lập phương

Công thức hiệu lập phương:

a³ – b³ = (a – b)(a² + ab + b²)

Ví dụ minh họa:

Tính 27³ – 8³ bằng công thức hằng đẳng thức:

a = 27, b = 8

a³ – b³ = (27 – 8)(27² + 27*8 + 8²) = 19*(729 + 216 + 64) = 19*1009 = 19171

Tổng lập phương

Công thức tổng lập phương:

a³ + b³ = (a + b)(a² – ab + b²)

Ví dụ minh họa:

Tính 9³ + 1³ bằng công thức:

a = 9, b = 1

a³ + b³ = (9 + 1)(9² – 9*1 + 1²) = 10*(81 – 9 + 1) = 10*73 = 730

 

Những công thức này rất hữu ích trong việc rút gọn biểu thức phức tạp hoặc phân tích đa thức thành nhân tử.

 

Cách áp dụng hằng đẳng thức bậc

Rút gọn biểu thức phức tạp

Các công thức hằng đẳng thức bậc 3 giúp rút gọn các biểu thức dạng lập phương nhanh chóng, tránh việc tính toán thủ công nhiều bước.

Ví dụ: Rút gọn x³ + 8:

x³ + 2³ = (x + 2)(x² – 2x + 4)

Như vậy, thay vì tính giá trị cụ thể, bạn có thể biểu diễn dưới dạng nhân tử.

Giải phương trình bậc 3 đơn giản

Các phương trình bậc 3 dạng x³ ± a³ = 0 có thể giải nhanh bằng hằng đẳng thức:

Ví dụ: Giải x³ – 27 = 0

x³ – 3³ = 0

(x – 3)(x² + 3x + 9) = 0

Suy ra nghiệm x = 3 hoặc nghiệm phức của phương trình bậc 2 x² + 3x + 9 = 0.

Phân tích đa thức thành nhân tử

Hằng đẳng thức bậc 3 giúp phân tích đa thức thành tích các biểu thức bậc 2 và bậc 1, rất quan trọng trong đại số.

Ví dụ: Phân tích x³ + 8x³y³

x³ + (2xy)³ = (x + 2xy)(x² – 2x²y + 4x²y²) 

Ứng dụng này giúp học sinh dễ dàng rút gọn hoặc giải phương trình phức tạp.

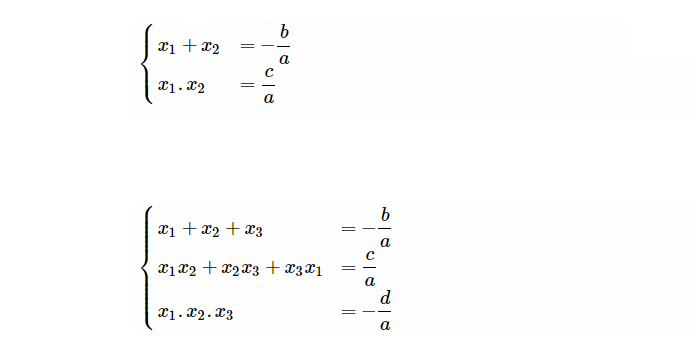
Ví dụ minh họa và bài tập vận dụng

Ví dụ rút gọn biểu thức

Rút gọn x³ + 27 bằng công thức tổng lập phương:

x³ + 3³ = (x + 3)(x² – 3x + 9)

Ví dụ giải phương trình

Giải x³ – 125 = 0

x³ – 5³ = 0

(x – 5)(x² + 5x + 25) = 0

Nghiệm x = 5 hoặc nghiệm phức của x² + 5x + 25 = 0.

Bài tập nâng cao

Rút gọn: 8a³ + 27b³ – 12ab(a + b)

8a³ + 27b³ – 12ab(a + b) = (2a + 3b)³ – 3*2a*3b*(2a + 3b) = (2a + 3b)³ – 18ab*(2a + 3b) 

= (2a + 3b)(4a² – 6ab + 9b²)

Những ví dụ này giúp học sinh ghi nhớ công thức đồng thời luyện tập rút gọn và giải phương trình nhanh chóng.

Lưu ý khi học hằng đẳng thức 

Phân biệt rõ các dạng tổng lập phương, hiệu lập phương.

Nhớ thứ tự nhân tử khi phân tích đa thức.

Kết hợp luyện tập với hằng đẳng thức bậc 2 để nhớ lâu hơn.

Lưu ý các lỗi thường gặp: nhầm dấu, quên nhân tử 3ab, sai thứ tự hạng tử.

Ứng dụng thực tế và nâng cao

Giải toán hình học liên quan đến thể tích và lập phương.

Luyện tập nâng cao cho học sinh giỏi, thi học sinh giỏi, ôn thi vào lớp 10.

Tính toán nhanh, rút gọn biểu thức phức tạp để tiết kiệm thời gian trong bài thi.

Mẹo học và ghi nhớ công thức hằng đẳng thức

Luyện tập viết công thức ra giấy nhiều lần để ghi nhớ nhanh.

Vẽ sơ đồ minh họa: (a + b)³, (a – b)³, a³ ± b³ để hình dung công thức.

So sánh với hằng đẳng thức bậc 2 để nhận biết điểm giống và khác.

Thường xuyên giải các bài tập rút gọn và phân tích đa thức.

Hằng đẳng thức  là kiến thức quan trọng trong toán học, từ lý thuyết đến ứng dụng thực tế. Nắm vững công thức:

Tổng lập phương: a³ + b³ = (a + b)(a² – ab + b²)

Hiệu lập phương: a³ – b³ = (a – b)(a² + ab + b²)

Lập phương tổng: (x + y)³ = x³ + y³ + 3xy(x + y)

Lập phương hiệu: (x – y)³ = x³ – y³ – 3xy(x – y)

Sẽ giúp học sinh rút gọn biểu thức, giải phương trình bậc 3, phân tích đa thức, và áp dụng vào các bài toán nâng cao. Việc luyện tập thường xuyên, kết hợp với hằng đẳng thức bậc 2 sẽ giúp học sinh ghi nhớ lâu, làm bài thi nhanh và chính xác.