Hệ Thức Lượng Trong Tam Giác Vuông: Công Thức, Bài Tập

Giới thiệu về hệ thức lượng trong tam giác 

 

Trong chương trình toán học phổ thông, đặc biệt là hình học lớp 9 và lớp 10, hệ thức lượng trong tam giác là một trong những nội dung quan trọng, gắn liền với nhiều dạng bài tập. Đây không chỉ là nền tảng để học sinh rèn luyện kỹ năng tư duy, giải toán chính xác, mà còn giúp áp dụng vào thực tế một cách linh hoạt.

 

Hệ thức lượng trong tam giác là tập hợp các công thức liên hệ giữa cạnh và góc của tam giác vuông. Những công thức này giúp học sinh dễ dàng tính toán cạnh còn thiếu, góc còn thiếu hoặc giải quyết nhanh các bài toán có liên quan đến chiều cao, diện tích, đường tròn ngoại tiếp…

 

Trong thực tế, hệ thức lượng trong tam giác vuông còn có nhiều ứng dụng, từ đo đạc, tính toán khoảng cách, chiều cao cho đến xây dựng công trình, thiết kế kỹ thuật. Vì vậy, việc nắm vững và ghi nhớ những công thức này là điều vô cùng quan trọng.

 

Trong bài viết này, chúng ta sẽ lần lượt tìm hiểu:

Các công thức cơ bản của hệ thức lượng trong tam giác vuông

Cách ghi nhớ nhanh, tránh nhầm lẫn

Những ứng dụng quan trọng trong toán học và đời sống

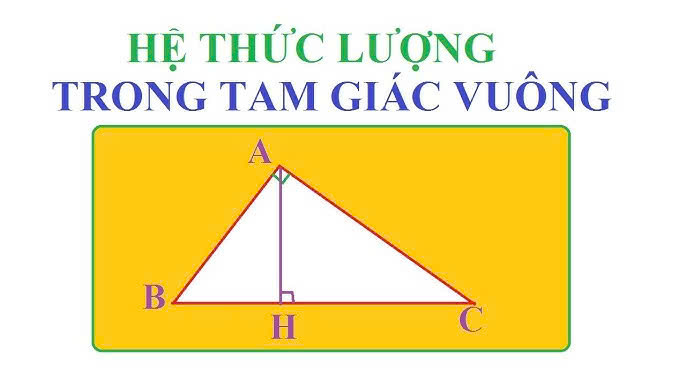
Các công thức hệ thức lượng trong tam giác 

 

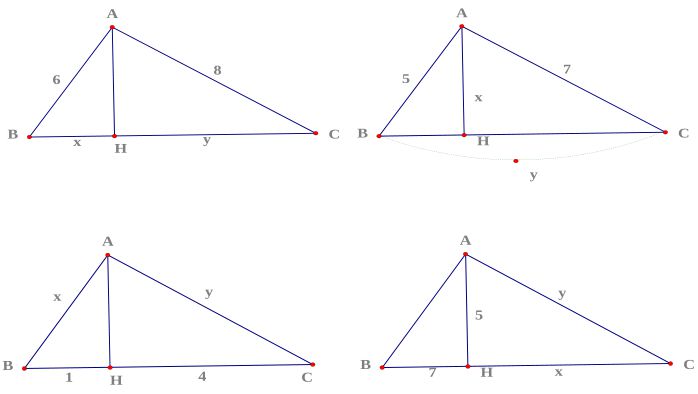
Giả sử ta có tam giác vuông ABC (vuông tại A), trong đó:

Cạnh huyền: BC = a

Cạnh góc vuông AB = c

Cạnh góc vuông AC = b

Đường cao AH vuông góc với BC (H là chân đường cao).

Từ đây ta có những hệ thức lượng cơ bản sau:

Hệ thức giữa cạnh và đường cao

a * h = b * c

Trong đó h là đường cao AH.

Hệ thức giữa cạnh và hình chiếu

b^2 = a * m

c^2 = a * n

Trong đó m = BH, n = HC.

Hệ thức liên hệ giữa đường cao và hình chiếu

h^2 = m * n

Hệ thức liên hệ giữa cạnh góc vuông và đường cao

b * c = a * h

Định lý Pythagore (công thức quan trọng nhất trong tam giác vuông)

a^2 = b^2 + c^2

 

Công thức diện tích tam giác vuông

S = 1/2 * b * c

S = 1/2 * a * h

Hệ thức liên quan đến đường tròn ngoại tiếp

Trong tam giác vuông, cạnh huyền chính là đường kính của đường tròn ngoại tiếp. Do đó:

R = a / 2 (R là bán kính đường tròn ngoại tiếp).

Tóm tắt các công thức hệ thức lượng trong tam giác vuông cần nhớ:

a^2 = b^2 + c^2

a * h = b * c

b^2 = a * m

c^2 = a * n

h^2 = m * n

S = 1/2 * b * c = 1/2 * a * h

R = a / 2

Những công thức trên xuất hiện liên tục trong đề kiểm tra, đề thi học kỳ và cả đề thi vào lớp 10, thi THPT quốc gia.

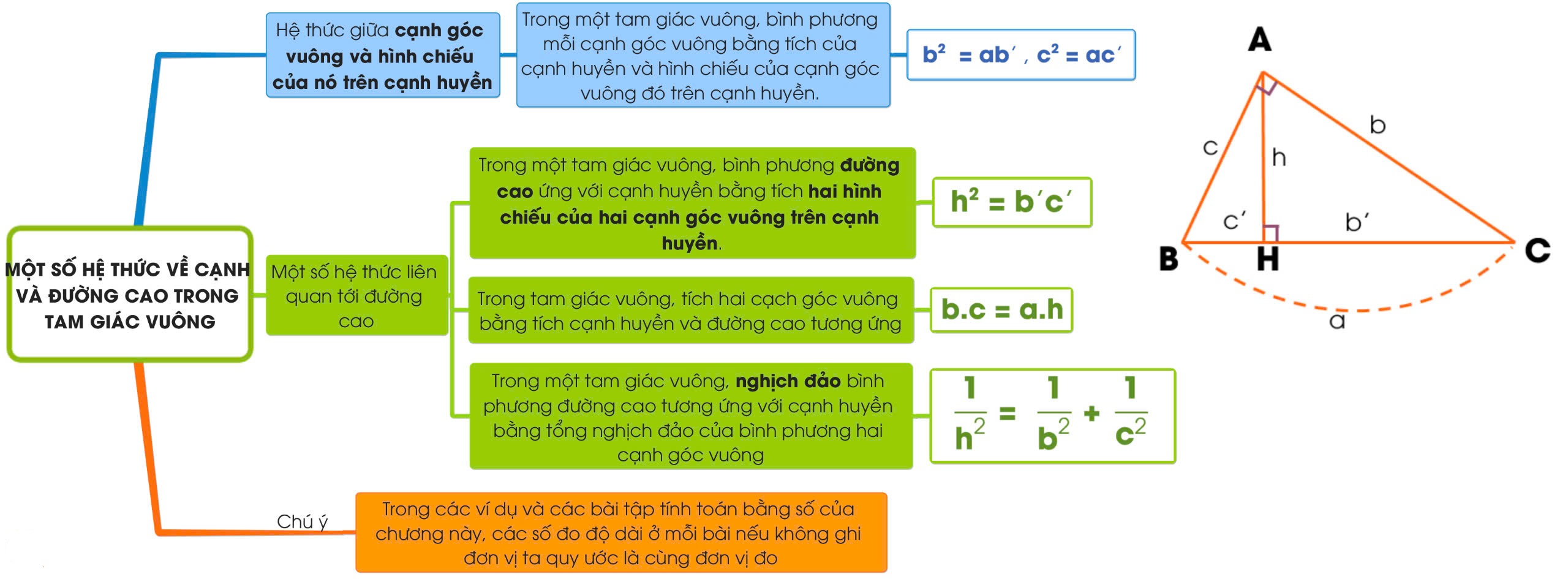
Cách ghi nhớ nhanh hệ thức lượng trong tam giác 

 

Vấn đề lớn nhất của học sinh khi học hệ thức lượng trong tam giác là… dễ nhầm lẫn. Nhiều bạn nhớ nhầm công thức hoặc nhầm ký hiệu dẫn đến kết quả sai. Dưới đây là một số mẹo giúp ghi nhớ dễ dàng và chính xác hơn:

Sử dụng định lý Pythagore làm nền tảng

Công thức a^2 = b^2 + c^2 là công thức gốc, bắt buộc phải nhớ. Khi đã nắm vững, các công thức khác dễ suy ra hơn.

 

Liên tưởng bằng hình ảnh

Vẽ tam giác vuông, đánh dấu cạnh huyền, đường cao, hình chiếu. Từ đó học công thức theo sơ đồ:

Cạnh góc vuông bình phương = cạnh huyền * hình chiếu tương ứng

Đường cao bình phương = tích hai hình chiếu

Cạnh huyền * đường cao = tích hai cạnh góc vuông

 

Mẹo ghi nhớ bằng câu nói ngắn

“Huyền bình phương bằng tổng bình phương hai cạnh góc vuông” (Pythagore).

“Cạnh góc vuông bình phương bằng huyền nhân hình chiếu” (công thức hình chiếu).

“Đường cao bình phương bằng tích hai hình chiếu” (công thức đường cao).

“Tích hai cạnh góc vuông bằng huyền nhân đường cao” (công thức cạnh và đường cao).

 

Học bằng ví dụ cụ thể

Ví dụ với tam giác vuông có cạnh b = 3, c = 4, thì a = 5 (tam giác 3-4-5 nổi tiếng).

Kiểm chứng Pythagore: 5^2 = 3^2 + 4^2 = 25 = 9 + 16.

Nếu hạ đường cao h từ A xuống BC: h = (b * c) / a = (3*4)/5 = 12/5 = 2.4

Hình chiếu m = b^2 / a = 9/5 = 1.8, n = c^2 / a = 16/5 = 3.2.

h^2 = 2.4^2 = 5.76 = m * n = 1.8 * 3.2.

Học theo ví dụ như vậy giúp nhớ lâu và hiểu bản chất công thức.

 

Ôn tập thường xuyên

Thay vì học dồn trước kỳ thi, hãy luyện tập mỗi ngày một vài bài. Khi công thức trở thành phản xạ, bạn sẽ không còn sợ nhầm lẫn.

Ứng dụng của hệ thức lượng trong toán học và thực tế

 

Hệ thức lượng trong tam giác không chỉ là kiến thức trên sách vở mà còn có nhiều ứng dụng quan trọng.

 

Ứng dụng trong toán học

 

Giải các bài toán về tính cạnh, tính góc trong tam giác vuông.

Giải bài toán liên quan đến đường tròn ngoại tiếp.

Chứng minh hình học.

Tính diện tích các hình phức tạp thông qua tam giác vuông.

Xuất hiện trong nhiều đề thi quan trọng.

 

Ứng dụng trong đo đạc thực tế

Khi muốn đo chiều cao của một vật thể mà không thể trèo lên, người ta có thể dùng hệ thức lượng trong tam giác vuông. Ví dụ: dựng cột mốc cách cây một đoạn, dùng thước đo góc rồi tính chiều cao bằng tam giác vuông.

 

Ứng dụng trong xây dựng và kiến trúc

Các công trình xây dựng như nhà ở, cầu đường, hay tháp đều sử dụng nguyên lý tam giác vuông để đo góc, tính độ dốc, xác định chiều cao. Công thức hệ thức lượng giúp đảm bảo công trình chính xác, cân đối.

 

Ứng dụng trong thiết kế và kỹ thuật

Trong ngành kỹ thuật cơ khí, điện tử, hệ thức lượng trong tam giác vuông được sử dụng để tính toán quỹ đạo, lực tác động, và nhiều yếu tố khác.

 

Ứng dụng trong đời sống hàng ngày

Đo chiều cao tòa nhà, ngọn núi, cây cổ thụ.

Tính khoảng cách từ điểm này đến điểm khác bằng phương pháp tam giác vuông.

Áp dụng trong định vị GPS, công nghệ bản đồ.

 

Ứng dụng trong khoa học hiện đại

Trong vật lý, công thức Pythagore và các hệ thức lượng tam giác vuông thường được dùng trong các bài toán về vận tốc, lực, hoặc xác định độ dài vectơ.

 

Hệ thức lượng trong tam giác vuông là một phần kiến thức quan trọng, vừa mang tính nền tảng, vừa có giá trị ứng dụng cao. Các công thức như a^2 = b^2 + c^2, b^2 = a * m, c^2 = a * n, h^2 = m * n không chỉ xuất hiện trong toán học phổ thông mà còn được áp dụng trong xây dựng, đo đạc, kỹ thuật và nhiều lĩnh vực khác.

Để học tốt, bạn cần ghi nhớ công thức bằng cách liên tưởng hình ảnh, học qua ví dụ cụ thể và luyện tập thường xuyên. Khi đã nắm vững, bạn sẽ thấy việc giải toán trở nên dễ dàng hơn, đồng thời có thể áp dụng kiến thức vào thực tế cuộc sống.

 

Hy vọng qua bài viết này, bạn đã có cái nhìn đầy đủ và chi tiết về hệ thức lượng trong tam giác vuông. Hãy luyện tập ngay hôm nay để biến công thức thành kỹ năng vững chắc.