Học Nhanh Công Thức Tính Chu Vi Hình Tròn

Giới thiệu chung về chu vi hình tròn

Trong hình học, hình tròn là một trong những hình cơ bản, quen thuộc và được ứng dụng rộng rãi trong thực tế — từ chiếc bánh xe, đồng hồ, đến miệng ly hay nắp nồi. Một trong những khái niệm quan trọng liên quan đến hình tròn chính là chu vi.

Chu vi hình tròn là độ dài đường bao quanh hình tròn. Nói cách khác, nếu bạn dùng một sợi dây để quấn tròn quanh một cái đĩa, rồi tháo ra và đo chiều dài sợi dây, bạn sẽ thu được giá trị chu vi của hình tròn đó.

Việc hiểu và biết cách tính chu vi hình tròn không chỉ giúp học tốt môn Toán mà còn rất hữu ích trong đời sống thực tế: từ việc tính chiều dài viền tường, ống nước, vành bánh xe cho đến các ứng dụng trong kỹ thuật, cơ khí và xây dựng. Chính vì vậy, nắm vững kiến thức về công thức tính chu vi hình tròn là nền tảng quan trọng trong học tập và làm việc.

Trong phần tiếp theo, chúng ta sẽ cùng tìm hiểu cách tính chu vi hình tròn chuẩn nhất, đi kèm ví dụ minh họa và những mẹo ghi nhớ cực dễ.

 

Công thức tính chu vi hình tròn chuẩn

Để tính chu vi của một hình tròn, chúng ta có thể sử dụng công thức cơ bản trong toán học như sau:

Chu vi hình tròn = 2 × π × r

Trong đó:

r là bán kính của hình tròn (khoảng cách từ tâm đến một điểm bất kỳ trên đường tròn).

π (đọc là “pi”) là một hằng số toán học, có giá trị xấp xỉ 3,14 hoặc 22/7 khi cần tính nhanh.

Công thức viết gọn:

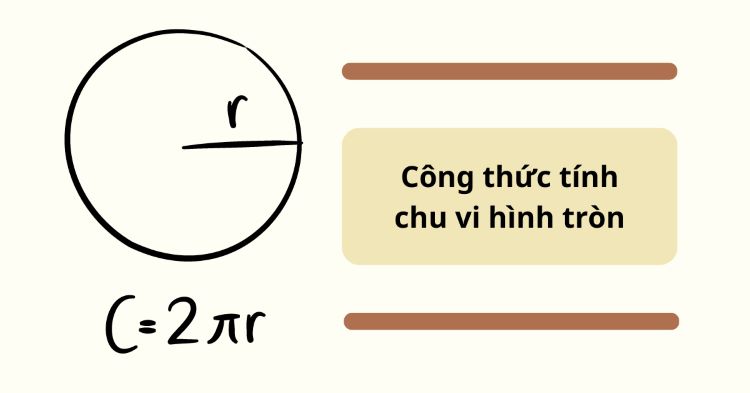
C = 2πr

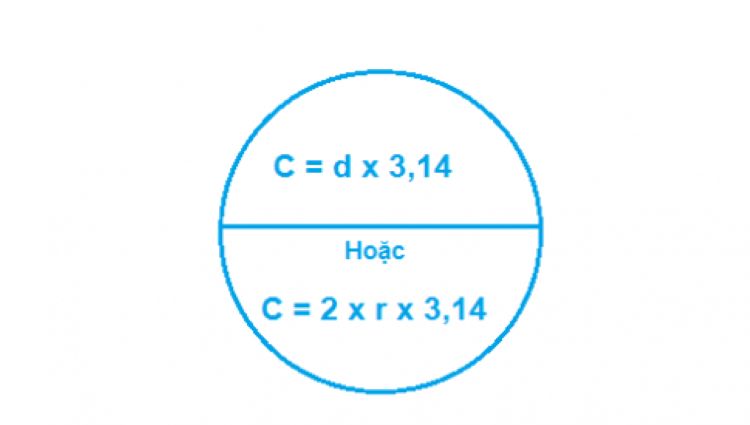
Hoặc nếu đề bài cho biết đường kính d thay vì bán kính, bạn cũng có thể dùng công thức tính chu vi hình tròn:

Chu vi hình tròn = π × d

Vì đường kính d = 2 × bán kính r, nên hai công thức hoàn toàn tương đương nhau.

Các lỗi sai thường gặp khi tính chu vi hình tròn

Dù công thức tính chu vi hình tròn khá đơn giản, nhưng nhiều người vẫn dễ mắc sai sót khi áp dụng vào thực tế hoặc làm bài tập. Dưới đây là một số lỗi sai phổ biến cần tránh:

 

Nhầm lẫn giữa bán kính (r) và đường kính (d)

Đây là lỗi phổ biến nhất. Nhiều người lấy giá trị đường kính nhưng lại áp dụng vào công thức 2πr mà không chia đôi để ra bán kính.

Ví dụ: Đề bài cho đường kính 10 cm, nhưng người học lại tính C = 2 × π × 10 = 62,8 cm, thay vì đúng phải là C = π × 10 = 31,4 cm hoặc C = 2 × π × 5.

 

Sử dụng sai giá trị của π (pi)

Một số bạn dùng π = 3 hoặc π = 3,1 khiến kết quả sai lệch nhiều.

Lời khuyên: nên dùng π = 3,14 hoặc π = 22/7 (nếu bán kính là số chia hết cho 7), hoặc dùng π trên máy tính để cho kết quả chính xác hơn.

 

Không ghi đơn vị hoặc sai đơn vị

Sau khi tính ra kết quả, nhiều người quên ghi đơn vị độ dài như cm, m, mm,… hoặc ghi sai đơn vị (như viết cm² thay vì cm).

Ghi nhớ: Chu vi luôn có đơn vị là độ dài, không phải diện tích.

 

Làm tròn kết quả sai cách

Làm tròn quá sớm trong quá trình tính toán có thể dẫn đến sai số lớn.

Hãy giữ kết quả trung gian càng chính xác càng tốt, chỉ làm tròn ở bước cuối cùng, nếu đề yêu cầu.

 

Quên nhân hệ số 2 trong công thức 2πr

Một số người chỉ lấy π × r hoặc π × d/2 do quên hệ số 2 trong công thức 2πr, dẫn đến kết quả bị thiếu một nửa.

 

Lời khuyên để tránh lỗi

Đọc kỹ đề bài xem cho bán kính hay đường kính.

Viết ra công thức trước khi thay số để dễ kiểm tra.

Ghi rõ đơn vị, làm tròn đúng yêu cầu đề bài.

Luôn soát lại xem kết quả có hợp lý với kích thước hình tròn hay không.

Mẹo ghi nhớ công thức tính chu vi hình tròn

Để ghi nhớ công thức chu vi hình tròn C = 2 × π × r một cách dễ dàng và lâu dài, bạn có thể áp dụng các mẹo sau:

Dùng câu vè, mẹo học thuộc đơn giản

“Hai pi r là chu vi, pi r bình là diện tích”

Đây là câu vè dân gian quen thuộc, giúp phân biệt được hai công thức dễ nhầm:

C = 2πr (Chu vi)

S = πr² (Diện tích)

Câu vè ngắn gọn, có vần, dễ học thuộc và thường được thầy cô sử dụng trong giảng dạy.

 

Hình ảnh hóa công thức

Hãy tưởng tượng một sợi dây quấn quanh một chiếc bánh (hình tròn). Độ dài sợi dây đó chính là chu vi.

Khi r là bán kính (từ tâm đến mép bánh), thì việc gấp đôi bán kính và nhân với π (3,14) sẽ ra độ dài đường tròn xung quanh – chính là công thức 2πr.

 

Ghi nhớ qua từ khóa

C – 2 – π – r: Tưởng tượng các chữ cái như một dãy mã PIN quen thuộc:

C là Chu vi → 2 lần → nhân với Pi (3,14) → nhân với r (bán kính).

 

So sánh với hình vuông để dễ liên tưởng

Hình vuông có chu vi là 4 × cạnh, tức 4 lần chiều dài.

Hình tròn không có cạnh, nhưng chu vi là 2 × bán kính × π, cho thấy nó cũng liên quan đến “độ dài xung quanh”.

Ứng dụng thực tế của công thức chu vi hình tròn

Công thức tính chu vi hình tròn C = 2 × π × r không chỉ xuất hiện trong sách giáo khoa Toán, mà còn được ứng dụng rất nhiều trong đời sống hằng ngày và các ngành nghề khác nhau. Dưới đây là những ví dụ điển hình:

 

Đo độ dài của các vật hình tròn

Khi muốn đo độ dài quanh mép của một vật hình tròn như: miệng ly, vòng tay, nắp hộp, bánh xe, đồng xu… bạn cần tính chu vi để biết được tổng chiều dài đường bao quanh.

Ví dụ: Bạn muốn bọc mép bàn tròn bằng cao su, tính chu vi sẽ giúp biết cần bao nhiêu mét dây cao su.

 

Tính toán trong xây dựng, cơ khí

Trong ngành xây dựng hoặc cơ khí, chu vi hình tròn được dùng để:

Tính chiều dài đường ống quấn quanh trục.

Xác định kích thước vòng đai, bánh răng hoặc vành xe.

Ước lượng vật liệu cần thiết để phủ kín mép hình tròn (sơn, inox, cao su, viền gạch…).

 

Thiết kế và sản xuất

Trong ngành thiết kế đồ họa, sản phẩm, hay thời trang, chu vi được dùng để:

Tính kích cỡ vòng cổ, vòng tay, vòng eo…

Thiết kế bao bì hình tròn hoặc bo tròn các cạnh.

 

Ứng dụng trong giao thông – vận tải

Dùng chu vi để tính:

Quãng đường bánh xe di chuyển trong một vòng quay (đặc biệt quan trọng với ô tô, xe máy, xe đạp).

Ví dụ: Biết chu vi bánh xe là 2,1 m → xe quay 1000 vòng = 2,1 km.

Ứng dụng trong đời sống hằng ngày

Tính chu vi để:

Biết kích thước bánh sinh nhật, in viền bánh, chia đều phần bánh.

Biết cần bao nhiêu vải để may váy dáng tròn, rèm cửa hình tròn.

Gói quà, cắt giấy tròn, thiết kế đồ chơi…