Số nguyên là gì: khái niệm, ví dụ và ứng dụng trong toán học
Số nguyên là gì là một trong những kiến thức cơ bản trong toán học, bao gồm các số dương, số âm và số 0. Việc nắm vững khái niệm này giúp học sinh giải quyết các bài toán về phép tính, sắp xếp số, cũng như áp dụng vào lập trình và đời sống. Cùng khám phá chi tiết qua bài viết dưới đây.
Số nguyên là gì
1.Khái niệm về số nguyên là gì trong toán học?
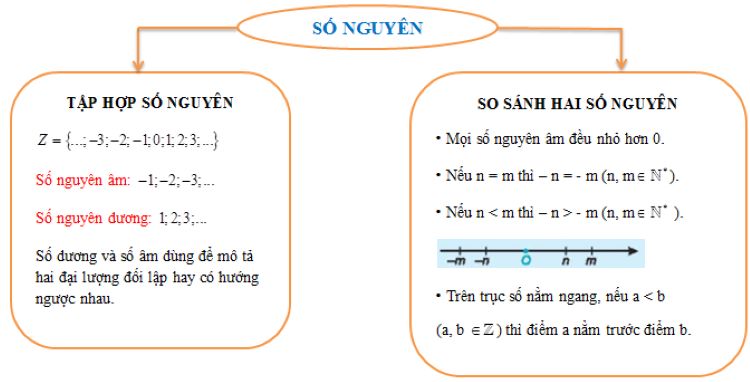
Số nguyên là gì? Số nguyên là tập hợp tất cả các số không có phần thập phân, bao gồm các số dương, số âm và số 0. Cụ thể, tập hợp số nguyên được chia thành ba nhóm chính:
- Số nguyên dương: 1, 2, 3, 4, …
- Số 0
- Số nguyên âm: -1, -2, -3, -4, …
Số nguyên là một khái niệm cơ bản và quan trọng trong toán học, bởi nó là nền tảng để thực hiện các phép toán cơ bản như cộng, trừ, nhân, đôi khi là chia (trong các trường hợp chia hết). Số nguyên cũng là cơ sở để học các kiến thức nâng cao trong đại số, số học, và các lĩnh vực toán học ứng dụng khác như lập trình, lý thuyết đồ thị, và thuật toán.
Việc nắm vững khái niệm số nguyên giúp học sinh và người học nhận diện đúng các loại số, thực hiện các phép tính chính xác và áp dụng linh hoạt vào giải quyết các bài toán lý thuyết cũng như các tình huống thực tế.

2.Làm sao để nhận biết một số là số nguyên hay không?
Để nhận biết một số có phải là số nguyên hay không, bạn cần hiểu rõ bản chất của số nguyên và áp dụng một số quy tắc cơ bản:
- Quan sát phần thập phân:Một số được coi là số nguyên nếu không có phần thập phân, nghĩa là số đó không có phần lẻ nào sau dấu phẩy. Ví dụ, các số …, -3, -2, -1, 0, 1, 2, 3, … đều là số nguyên, trong khi 4,5 hay -1,2 không phải là số nguyên.
- Kiểm tra bằng phép chia:Một số nguyên khi chia cho 1 sẽ không dư. Nếu số đó chia cho 1 mà còn phần dư, thì nó không phải là số nguyên.
- So sánh với số nguyên gần nhất:Nếu số đó khớp hoàn toàn với một số nguyên mà không phải làm tròn, thì nó là số nguyên. Cách này đặc biệt hữu ích khi làm việc với số lớn hoặc trong lập trình.
- Quan sát dấu và giá trị:Số nguyên có thể âm, dương hoặc bằng 0. Như vậy, tất cả các số âm, số dương hoặc 0 không có phần thập phân đều là số nguyên.
Ví dụ minh họa:
- 7 → số nguyên
- -5 → số nguyên
- 0 → số nguyên
- 3,14 → không phải số nguyên
- -2,7 → không phải số nguyên
Nhờ những quy tắc này, bạn có thể nhận biết một số là số nguyên hay không một cách chính xác và nhanh chóng, từ đó áp dụng hiệu quả trong giải bài tập toán, lập trình hoặc các tình huống thực tế liên quan đến số học.
3.Tại sao việc nắm vững số nguyên lại quan trọng trong toán học?
Việc nắm vững khái niệm số nguyên là rất quan trọng trong toán học vì số nguyên là một trong những loại số cơ bản nhất và là nền tảng để học các kiến thức nâng cao hơn.
- Cơ sở để học các phép toán cơ bản: Số nguyên giúp thực hiện các phép cộng, trừ, nhân, chia trong nhiều bài toán từ đơn giản đến phức tạp.
- Phát triển tư duy logic và suy luận: Việc phân loại, nhận biết và tính toán với số nguyên rèn luyện khả năng tư duy logic, phân tích và giải quyết vấn đề.
- Ứng dụng trong các lĩnh vực khác: Số nguyên được dùng trong đại số, số học, lập trình, lý thuyết đồ thị, thuật toán và các ứng dụng khoa học kỹ thuật khác.
- Làm nền tảng cho các kiến thức nâng cao: Hiểu rõ về số nguyên giúp học sinh tiếp cận dễ dàng hơn với các kiến thức về số hữu tỉ, số thực, phương trình, bất phương trình và các bài toán liên quan.
- Áp dụng trong đời sống thực tế: Số nguyên xuất hiện trong đo lường, đếm, xác định mức độ, thứ tự, lập kế hoạch và nhiều tình huống thực tế khác.
Nhờ nắm vững khái niệm và cách vận dụng số nguyên, học sinh và người học có thể giải quyết các bài toán toán học một cách chính xác, hiệu quả và áp dụng linh hoạt trong thực tế, đồng thời tạo nền tảng vững chắc để học các kiến thức toán học nâng cao hơn.

4.Các dạng bài tập áp dụng số nguyên trong toán học
Số nguyên là một trong những kiến thức cơ bản nhất trong toán học, được sử dụng trong nhiều dạng bài tập khác nhau từ đơn giản đến nâng cao. Dưới đây là một số dạng phổ biến:
- Bài tập nhận biết số nguyên:
Xác định một số cho trước có phải là số nguyên hay không dựa trên tính chất không có phần thập phân.
Ví dụ: -5, 0, 3, 2,7 → nhận biết số nguyên và số không phải số nguyên. - Bài tập so sánh và sắp xếp số nguyên:
So sánh hai hoặc nhiều số nguyên và sắp xếp chúng theo thứ tự tăng dần hoặc giảm dần.
Ví dụ: Sắp xếp các số -3, 7, 0, -1, 5 theo thứ tự tăng dần → -3, -1, 0, 5, 7 - Bài tập phép tính với số nguyên:
Thực hiện các phép cộng, trừ, nhân, chia với số nguyên.
Ví dụ: (-3) + 7 = 4, 5 – (-2) = 7, (-4) × 3 = -12 - Bài tập ứng dụng số nguyên trong thực tế:
Dùng số nguyên để biểu thị nhiệt độ, độ cao, nợ- có, hoặc các giá trị âm và dương trong đời sống.
Ví dụ: Nhiệt độ hôm nay là -2°C, hôm qua là 3°C → tính độ chênh lệch nhiệt độ. - Bài tập giải phương trình, bất phương trình với số nguyên:
Tìm nghiệm nguyên của phương trình hoặc bất phương trình.
Ví dụ: Tìm x ∈ Z thỏa mãn 2x + 5 = 11 → x = 3 - Bài tập nâng cao kết hợp nhiều phép toán:
Kết hợp nhận biết, sắp xếp, so sánh, và tính toán với số nguyên trong cùng một bài toán.
Ví dụ: Một người đi lên 5 tầng, xuống 3 tầng, sau đó lên thêm 2 tầng. Hỏi vị trí cuối cùng so với tầng xuất phát.
Nhờ việc luyện tập các dạng bài tập trên, học sinh sẽ nắm chắc khái niệm số nguyên, thực hiện phép tính chính xác, rèn luyện tư duy logic và áp dụng linh hoạt vào các bài toán nâng cao hoặc tình huống thực tế.
5.Số nguyên có ứng dụng gì trong lập trình hoặc khoa học máy tính?
Số nguyên là một trong những kiểu dữ liệu cơ bản và quan trọng trong lập trình và khoa học máy tính. Chúng được sử dụng rộng rãi để biểu diễn, tính toán và xử lý dữ liệu.
- Lưu trữ và tính toán: Số nguyên dùng để lưu các giá trị không thập phân, ví dụ như đếm số lần lặp, đánh số thứ tự, hoặc tính toán các chỉ số mảng.
- Điều kiện và vòng lặp: Trong các vòng lặp for, while, số nguyên thường được dùng làm biến điều khiển, xác định số lần thực hiện của vòng lặp.
- Thuật toán và cấu trúc dữ liệu: Số nguyên được dùng trong các thuật toán tìm kiếm, sắp xếp, và các cấu trúc dữ liệu như mảng, danh sách liên kết, ngăn xếp, hàng đợi.
- Biểu diễn trạng thái: Trong lập trình trò chơi, mô phỏng hay robot, số nguyên dùng để biểu diễn trạng thái, điểm số, tọa độ rời rạc hoặc các chỉ số trạng thái.
- Toán học máy tính: Số nguyên là cơ sở để tính toán số học, xử lý đồ họa, mật mã học, và các thuật toán số học lớn (big integer).
Nhờ việc sử dụng số nguyên, lập trình viên và nhà khoa học máy tính có thể xử lý dữ liệu chính xác, hiệu quả, và lập các thuật toán phức tạp một cách nhanh chóng và an toàn.
Trên đây chúng tôi đã cùng bạn tìm hiểu chi tiết về số nguyên là gì, từ khái niệm cơ bản, cách nhận biết, phân loại, đến các dạng bài tập áp dụng trong toán học và các ví dụ thực tế. Việc nắm vững kiến thức về số nguyên không chỉ giúp giải quyết các bài toán hình học và số học chính xác mà còn tạo nền tảng vững chắc cho việc học các kiến thức toán học nâng cao và lập trình máy tính.
Hy vọng bài viết số nguyên là gì đã mang đến cho bạn những thông tin bổ ích, giúp dễ dàng áp dụng số nguyên vào học tập, giải toán và các ứng dụng thực tế hàng ngày.
Có thể bạn quan tâm:

Đại lý sơn nước chính hãng Thái Bình Dương
Chúng tôi luôn mong muốn mang đến giá trị cho cộng đồng chính là mang lại niềm tin trong tiêu dùng. Khách hàng có trải nghiệm mua sắm tuyệt vời. Hotline 0865.663.918 hoặc hòm thư: ngloan2712@gmail.com






