Số Nguyên Là Gì? Kiến Thức Nền Tảng Trong Toán Học

Giới thiệu về số nguyên

Số nguyên là một khái niệm cơ bản trong toán học, xuất hiện trong hầu hết các chương trình học từ tiểu học đến trung học. Đây là một tập hợp số bao gồm các số nguyên dương, số nguyên âm và số 0.

 

Khái niệm số nguyên là gì?

Số nguyên là những số:

Không có phần thập phân (sau dấu phẩy)

Không có phần lẻ, không phải là phân số

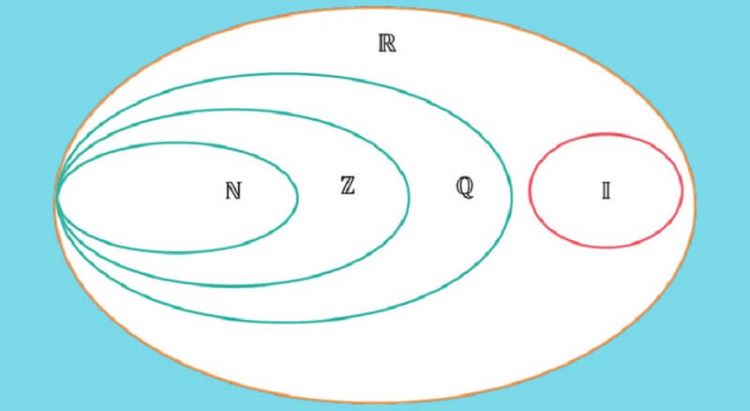
Tập hợp các số nguyên là gì thường được ký hiệu là ℤ, bao gồm:

…, -3, -2, -1, 0, 1, 2, 3, …

Định nghĩa số nguyên là gì?

Số nguyên là tập hợp các số không có phần thập phân, bao gồm:

Số nguyên âm (… −3, −2, −1)

Số 0

Số nguyên dương (1, 2, 3, …)

Tập hợp số nguyên được ký hiệu là ℤ (viết tắt từ tiếng Đức Zahlen, nghĩa là “các số”).

Ví dụ về số nguyên

Số nguyên dương: 5, 12, 100

Số nguyên âm: −7, −21, −100

Số 0: cũng là một số nguyên

Lưu ý:

Các số như 2.5, -3.1, ½ không phải là số nguyên, vì chúng có phần thập phân hoặc là phân số.

Số nguyên là nền tảng cơ bản trong Toán học và được dùng rộng rãi trong thực tế như: tính toán nhiệt độ, độ cao, tài chính (lãi/lỗ), thời gian (quá khứ – tương lai)…

 

Phân loại số nguyên

Số nguyên dương

Là các số lớn hơn 0

Không có dấu “–” phía trước

Ví dụ: 1, 2, 3, 10, 100…

Ký hiệu: thuộc ℤ⁺ hoặc đôi khi là ℕ (tập hợp số tự nhiên, không bao gồm số 0 nếu không có quy định riêng)

 

Số nguyên âm

Là các số nhỏ hơn 0

Có dấu “–” phía trước

Ví dụ: –1, –2, –10, –100…

 Ký hiệu: thuộc ℤ⁻

 

Số 0

Là số trung tính trong tập hợp số nguyên

Không phải số dương cũng không phải số âm

Đóng vai trò là điểm phân chia giữa số nguyên dương và số nguyên âm trên trục số

Các phép toán với số nguyên

Số nguyên cho phép thực hiện đầy đủ bốn phép toán cơ bản: cộng, trừ, nhân, chia. Tuy nhiên, khi tính toán với số nguyên âm và dương, bạn cần nắm rõ quy tắc dấu.

Phép cộng số nguyên

Cùng dấu: cộng hai giá trị tuyệt đối, giữ nguyên dấu

▸ Ví dụ: (–3) + (–5) = –8

▸ 2 + 7 = 9

Khác dấu: lấy số lớn trừ số nhỏ, giữ dấu của số có giá trị tuyệt đối lớn hơn

▸ Ví dụ: (–8) + 5 = –3

▸ (–2) + 9 = 7

 

Phép trừ số nguyên

Trừ một số là cộng với số đối của nó

▸ Ví dụ: 5 – (–3) = 5 + 3 = 8

▸ (–6) – (2) = –6 + (–2) = –8

 

Phép nhân số nguyên

Cùng dấu → kết quả là số dương

▸ Ví dụ: (–4) × (–3) = 12

▸ 2 × 5 = 10

 

Khác dấu → kết quả là số âm

▸ Ví dụ: (–7) × 2 = –14

 

Phép chia số nguyên

Cùng dấu → kết quả là số dương

▸ (–12) ÷ (–3) = 4

 

Khác dấu → kết quả là số âm

▸ 15 ÷ (–5) = –3

 

 Lưu ý:

Phép chia hai số nguyên là gì không phải lúc nào cũng cho ra một số nguyên (ví dụ: 7 ÷ 2 = 3.5 không phải số nguyên).

Nếu đề bài yêu cầu “kết quả là số nguyên”, bạn cần làm tròn hoặc chỉ xét các phép chia hết.

Lưu ý thường gặp khi học số nguyên

Việc học số nguyên là gì thường gặp một số lỗi phổ biến do nhầm lẫn về dấu, quy tắc tính, hoặc khái niệm chưa rõ ràng. Dưới đây là những lưu ý quan trọng giúp bạn học số nguyên hiệu quả hơn:

 

Cẩn thận với dấu cộng (+) và trừ (–)

Nhiều bạn nhầm lẫn giữa dấu của số và phép toán.

▸ Ví dụ: (–5) – (–3) rất khác với (–5) – 3

 

Mẹo: Khi có dấu ngoặc, đổi dấu và áp dụng đúng quy tắc cộng trừ số nguyên.

 

Hiểu rõ mối quan hệ giữa trừ và cộng

Phép trừ có thể chuyển thành phép cộng số đối:

▸ A – B = A + (–B)

▸ Ví dụ: 6 – (–2) = 6 + 2 = 8

 

Nhớ quy tắc dấu khi nhân và chia

Cùng dấu → kết quả dương

 

Khác dấu → kết quả âm

▸ Ví dụ: (–4) × (–3) = 12, nhưng (–4) × 3 = –12

 

Không nhầm lẫn số nguyên với số thập phân hoặc phân số

Số nguyên không có phần thập phân hoặc phân số.

▸ Ví dụ: –2 là số nguyên, nhưng –2.5 không phải.

 

Biết rằng số 0 là một số nguyên đặc biệt

0 không thuộc nhóm dương hay âm, nhưng vẫn là số nguyên.

Nhiều người nhầm rằng 0 là số dương hoặc âm, điều này là sai.

 

Luyện vẽ trục số để trực quan hơn

Trục số giúp hình dung được vị trí của các số nguyên (âm ở bên trái 0, dương ở bên phải).

Đây là cách học trực quan rất hiệu quả cho người mới bắt đầu.

 

Tập luyện thường xuyên với bài tập nhỏ

Làm các bài toán đơn giản rồi nâng dần độ khó sẽ giúp ghi nhớ quy tắc tốt hơn.

Nên luyện với phép cộng, trừ có ngoặc hoặc nhiều dấu xen kẽ.

Khi học số nguyên là gì, hãy tập trung vào quy tắc dấu, hiểu rõ khái niệm số đối, luyện tập các phép toán cơ bản và tránh nhầm lẫn giữa ký hiệu và phép tính. Nắm vững những lưu ý trên sẽ giúp bạn học nhanh và chắc chắn hơn.