Số nguyên là gì? Ứng dụng của số nguyên trong toán học

Số nguyên là gì

Số nguyên là gì? Đây là câu hỏi mở đầu cho một khái niệm toán học cơ bản nhưng vô cùng quan trọng trong các lĩnh vực khoa học và đời sống. Trong bài viết này, chúng ta sẽ tìm hiểu sâu hơn về số nguyên, phân loại các số nguyên và khám phá ứng dụng của chúng.

1.Số nguyên là gì?

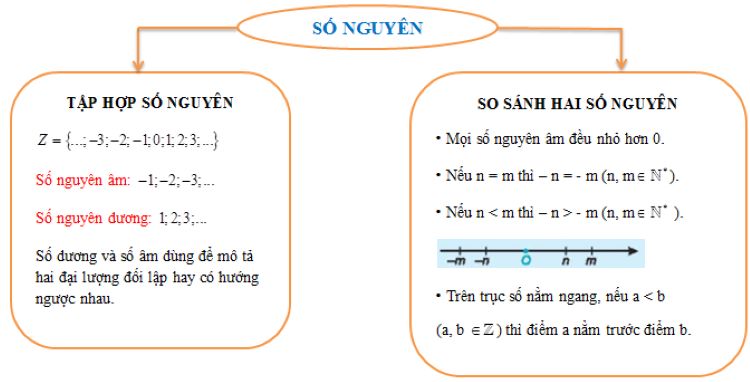
Số nguyên là gì? Số nguyên là một tập hợp các số bao gồm các số dương, âm và số 0. Tập hợp số nguyên được ký hiệu là Z, trong đó:

• Số nguyên dương (hay số tự nhiên dương): Các số lớn hơn 0, ví dụ: 1, 2, 3, 4, …
• Số nguyên âm: Các số nhỏ hơn 0, ví dụ: -1, -2, -3, -4, …
• Số 0: Là một số nguyên đặc biệt không phải là số dương hay số âm.

Tập hợp số nguyên bao gồm các số như: …,−3,−2,−1,0,1,2,3,…

Số nguyên được sử dụng rộng rãi trong nhiều lĩnh vực toán học, khoa học, kinh tế và cuộc sống hàng ngày để biểu diễn các giá trị như số lượng, mức độ, sự thay đổi (tăng giảm), và nhiều ứng dụng khác.

2.Tính chất cơ bản của số nguyên

Các tính chất cơ bản của số nguyên bao gồm một số đặc điểm quan trọng liên quan đến các phép toán như cộng, trừ, nhân, chia. Dưới đây là các tính chất cơ bản:

Tính chất đóng của số nguyên đối với phép cộng và phép nhân

• Cộng: Tập hợp số nguyên là đóng đối với phép cộng. Điều này có nghĩa là khi cộng hai số nguyên, kết quả luôn là một số nguyên.
  • Ví dụ: 3+(−5)=−2 hoặc −3+6=3.
• Nhân: Tập hợp số nguyên cũng là đóng đối với phép nhân. Khi nhân hai số nguyên, kết quả luôn là một số nguyên.
  • Ví dụ: 3×(−4)=−12 hoặc −2×5=−10.

Tính chất kết hợp của phép cộng và phép nhân

• Cộng: Phép cộng số nguyên thỏa mãn tính chất kết hợp, nghĩa là bạn có thể thay đổi thứ tự nhóm các số mà không làm thay đổi kết quả.
  • Ví dụ: (2+3)+4=2+(3+4).
• Nhân: Phép nhân số nguyên cũng thỏa mãn tính chất kết hợp.
  • Ví dụ: (2×3)×4=2×(3×4)).

Tính chất giao hoán của phép cộng và phép nhân

• Cộng: Phép cộng số nguyên thỏa mãn tính chất giao hoán, tức là bạn có thể thay đổi thứ tự của các số mà không thay đổi kết quả.
  • Ví dụ: 2+3=3+22.
• Nhân: Phép nhân số nguyên cũng thỏa mãn tính chất giao hoán.
  • Ví dụ: 2×3=3×2.

Tính chất phân phối của phép nhân đối với phép cộng

• Phép nhân số nguyên phân phối đối với phép cộng, nghĩa là bạn có thể nhân từng phần trong biểu thức trước khi cộng.
  • Ví dụ: a×(b+c)=a×b+a×c.

Phần tử trung hòa của phép cộng và phép nhân

• Cộng: Số 0 là phần tử trung hòa trong phép cộng. Khi cộng số 0 với bất kỳ số nguyên nào, kết quả sẽ là chính số đó.
  • Ví dụ: 3+0=3 và 0+(−5)=−5.
• Nhân: Số 1 là phần tử trung hòa trong phép nhân. Khi nhân bất kỳ số nguyên nào với 1, kết quả sẽ là chính số đó.
  • Ví dụ: 4×1=4 và (−7)×1=−7.

Đối ngược của số nguyên

• Mỗi số nguyên đều có một số đối ngược (hoặc đối số), là số có giá trị tuyệt đối giống nhưng dấu ngược lại.
  • Ví dụ: Số đối ngược của 3 là −3, và số đối ngược của −5 là 5.

Tính chất phân biệt giữa số nguyên và số tự nhiên

• Số nguyên bao gồm cả số dương, số âm và số 0, trong khi số tự nhiên chỉ bao gồm các số dương từ 1 trở lên. Số 0 là một phần của số nguyên nhưng không phải là số tự nhiên.

Không đóng đối với phép chia

• Chia: Tập hợp số nguyên không đóng đối với phép chia, nghĩa là khi chia hai số nguyên, kết quả chưa chắc chắn là một số nguyên. Ví dụ: 5÷2=2.5, nhưng 2.5 không phải là số nguyên.

Tính chất so sánh

• Các số nguyên có thể được so sánh với nhau bằng các dấu so sánh như =, <, >.
  • Ví dụ: −3<2, 0=0, 5>−1.

Các tính chất cơ bản của số nguyên giúp định hình cách thức sử dụng chúng trong các phép toán và lý thuyết toán học. Những tính chất này là nền tảng quan trọng để giải quyết các bài toán và ứng dụng số nguyên trong nhiều lĩnh vực khác nhau.

3.Phân loại số nguyên

Số nguyên có thể được phân loại thành các nhóm sau:

Số nguyên dương

• Khái niệm: Số nguyên dương là các số nguyên lớn hơn 0.
• Ví dụ: 1,2,3,4,5,….
• Đặc điểm: Các số này thường được sử dụng để chỉ số lượng hoặc giá trị tích cực trong thực tế (như số người, số vật thể, v.v.).

Số nguyên âm

• Khái niệm: Số nguyên âm là các số nguyên nhỏ hơn 0.
• Ví dụ: −1,−2,−3,−4,−5,….
• Đặc điểm: Các số này được dùng để biểu thị các giá trị giảm, thâm hụt hoặc các khái niệm ngược lại của các giá trị dương (như nhiệt độ dưới 0 độ C, lỗ hổng trong ngân sách, v.v.).

Số 0

• Khái niệm: 0 là một số nguyên đặc biệt, nó không phải là số dương cũng không phải là số âm.
• Ví dụ: 0.
• Đặc điểm: Số 0 đóng vai trò trung hòa trong phép cộng (bởi vì a+0=a với mọi số nguyên a) và không có số đối ngược trong phép nhân (bởi vì a×0=0 với mọi số nguyên a).

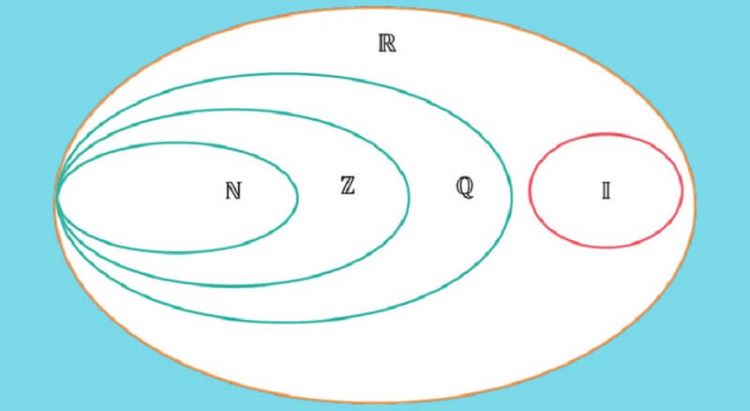
Số nguyên trong tập hợp

• Tập hợp số nguyên, ký hiệu là Z, bao gồm tất cả các số nguyên dương, âm và 0.
• Ví dụ: Tập hợp số nguyên có dạng: …,−3,−2,−1,0,1,2,3,…

Tóm lại:

Số nguyên có thể được phân loại thành ba loại chính:

• Số nguyên dương: Các số lớn hơn 0.
• Số nguyên âm: Các số nhỏ hơn 0.
• Số 0: Là số đặc biệt không phải là dương hay âm, đóng vai trò trung hòa.

4.Ứng dụng của số nguyên trong toán học

Số nguyên có rất nhiều ứng dụng quan trọng trong toán học, giúp giải quyết các bài toán liên quan đến các phép toán cơ bản, lý thuyết số, và các lĩnh vực khác. Dưới đây là một số ứng dụng của số nguyên trong toán học:

Các phép toán cơ bản

• Cộng, trừ, nhân, chia: Số nguyên là cơ sở để thực hiện các phép toán cơ bản trong toán học. Tính toán các giá trị tổng, hiệu, tích, và thương của các số nguyên giúp giải quyết nhiều bài toán trong các lĩnh vực khác nhau.
  • Ví dụ: Tính toán tổng của các số nguyên trong dãy số, tìm hiệu giữa các số nguyên.

Lý thuyết số

• Định lý chia hết: Số nguyên được sử dụng trong lý thuyết số để kiểm tra tính chia hết của một số. Các khái niệm như số chẵn, số lẻ, tính chất chia hết, và ước chung lớn nhất (UCLN), bội chung nhỏ nhất (BCNN) đều liên quan đến số nguyên.
  • Ví dụ: Kiểm tra xem số 36 có chia hết cho 6 hay không, tìm UCLN và BCNN của các số nguyên.

Giải phương trình và bất phương trình

• Số nguyên thường được sử dụng trong việc giải các phương trình và bất phương trình. Các bài toán có nghiệm là số nguyên sẽ có ứng dụng đặc biệt trong nhiều lĩnh vực toán học như đại số, giải tích, v.v.
  • Ví dụ: Giải phương trình bậc 1 với nghiệm là số nguyên, hoặc tìm nghiệm của các bất phương trình có nghiệm là số nguyên.

Dãy số và chuỗi số

• Số nguyên là thành phần chính trong các dãy số và chuỗi số. Các dãy số như dãy số tự nhiên, dãy số nguyên liên tiếp, dãy số đối xứng đều là ví dụ điển hình.
  • Ví dụ: Tính tổng các phần tử trong dãy số, xác định số hạng tổng quát của dãy số nguyên.

Phân tích số nguyên

• Số nguyên được sử dụng trong phân tích số nguyên để tìm các đặc điểm của các số như số nguyên tố, phân tích ra thừa số nguyên tố, v.v.
  • Ví dụ: Phân tích số nguyên 30 ra thừa số nguyên tố là 2×3×5.

Giải bài toán tối ưu

• Trong tối ưu hóa và lý thuyết đồ thị, số nguyên là yếu tố quan trọng khi giải các bài toán về tối ưu số nguyên, tìm giá trị nhỏ nhất hoặc lớn nhất trong các bài toán mà nghiệm phải là số nguyên.
  • Ví dụ: Tìm giá trị tối ưu cho bài toán phân bổ nguồn lực, bài toán lựa chọn trong lập lịch.

Sử dụng trong hệ thống tọa độ

• Số nguyên được sử dụng trong hệ thống tọa độ Descartes, đặc biệt là trong các hệ thống tọa độ một chiều, hai chiều, hoặc ba chiều. Mỗi điểm trên trục số có thể là một số nguyên.
  • Ví dụ: Xác định vị trí của các điểm trong mặt phẳng với tọa độ là các số nguyên.

Biểu diễn các khái niệm trong lý thuyết đồ thị

• Trong lý thuyết đồ thị, số nguyên thường được sử dụng để biểu diễn các đỉnh và các cạnh của đồ thị, đồng thời xác định số lượng đỉnh, cạnh trong đồ thị.
  • Ví dụ: Xác định số cạnh trong một đồ thị đầy đủ hoặc số đỉnh trong đồ thị Euler.

Lý thuyết đồng dư

• Số nguyên có ứng dụng rộng rãi trong lý thuyết đồng dư, giúp giải quyết các bài toán liên quan đến phép chia và tìm số dư khi chia một số nguyên cho một số nguyên khác.
  • Ví dụ: Giải các bài toán về đồng dư, như tìm x sao cho x≡3 (mod 5).

Số nguyên trong xác suất và thống kê

• Trong xác suất và thống kê, số nguyên được sử dụng để biểu thị số lượng sự kiện hoặc mẫu, chẳng hạn trong các bài toán xác suất rời rạc, phân phối xác suất.
  • Ví dụ: Xác định số khả năng xuất hiện của các sự kiện trong trò chơi may rủi hoặc xác suất phân phối của một biến ngẫu nhiên.

Số nguyên trong lý thuyết nhóm và lý thuyết đại số

• Lý thuyết nhóm và các lý thuyết đại số khác cũng sử dụng số nguyên để biểu diễn các phần tử nhóm, cấu trúc đại số và các phép toán trong không gian đại số.
  • Ví dụ: Phân tích các phép toán nhóm trong không gian số nguyên và các phép toán đồng nhất.

Tóm lại:

Số nguyên là gì? Số nguyên là một phần không thể thiếu trong toán học, với các ứng dụng từ các phép toán cơ bản đến lý thuyết phức tạp, như lý thuyết số, phân tích dãy số, lý thuyết đồ thị, và nhiều lĩnh vực khác. Sự đa dạng trong các ứng dụng của số nguyên cho thấy vai trò quan trọng của chúng trong việc giải quyết các vấn đề toán học và thực tiễn.

Bài viết trên đã giải đáp cho câu hỏi Số nguyên là gì và cung cấp những thông tin hữu ích về khái niệm, tính chất, phân loại cũng như ứng dụng của số nguyên trong nhiều lĩnh vực khác nhau. Hy vọng qua bài viết, bạn đã có cái nhìn rõ ràng hơn về số nguyên và vai trò của chúng trong toán học và thực tiễn. Nếu bạn đang tìm kiếm sự tư vấn về màu sơn và loại sơn phù hợp cho công trình của mình, hãy liên hệ với sonthaibinhduong.com để được hỗ trợ và tư vấn chi tiết.

CÔNG TY TNHH THƯƠNG MẠI ĐẦU TƯ SƠN PACIFIC

Hotline/Zalo: 0865663918

Địa chỉ Showroom 1: 269 Vườn Lài, P. Phú Thọ Hòa, Q.Tân Phú, TP.HCM

Địa chỉ Showroom 2: 243 Tô Ký, Ấp Mới, Trung Chánh, Hóc Môn, TP.HCM

Website: https://sonthaibinhduong.com/