Các Hệ Thức Lượng Trong Tam Giác Vuông Lớp 9 Chi Tiết

1. Các hệ thức lượng giác trong tam giác vuông

Hệ thức liên quan về cạnh và đường cao
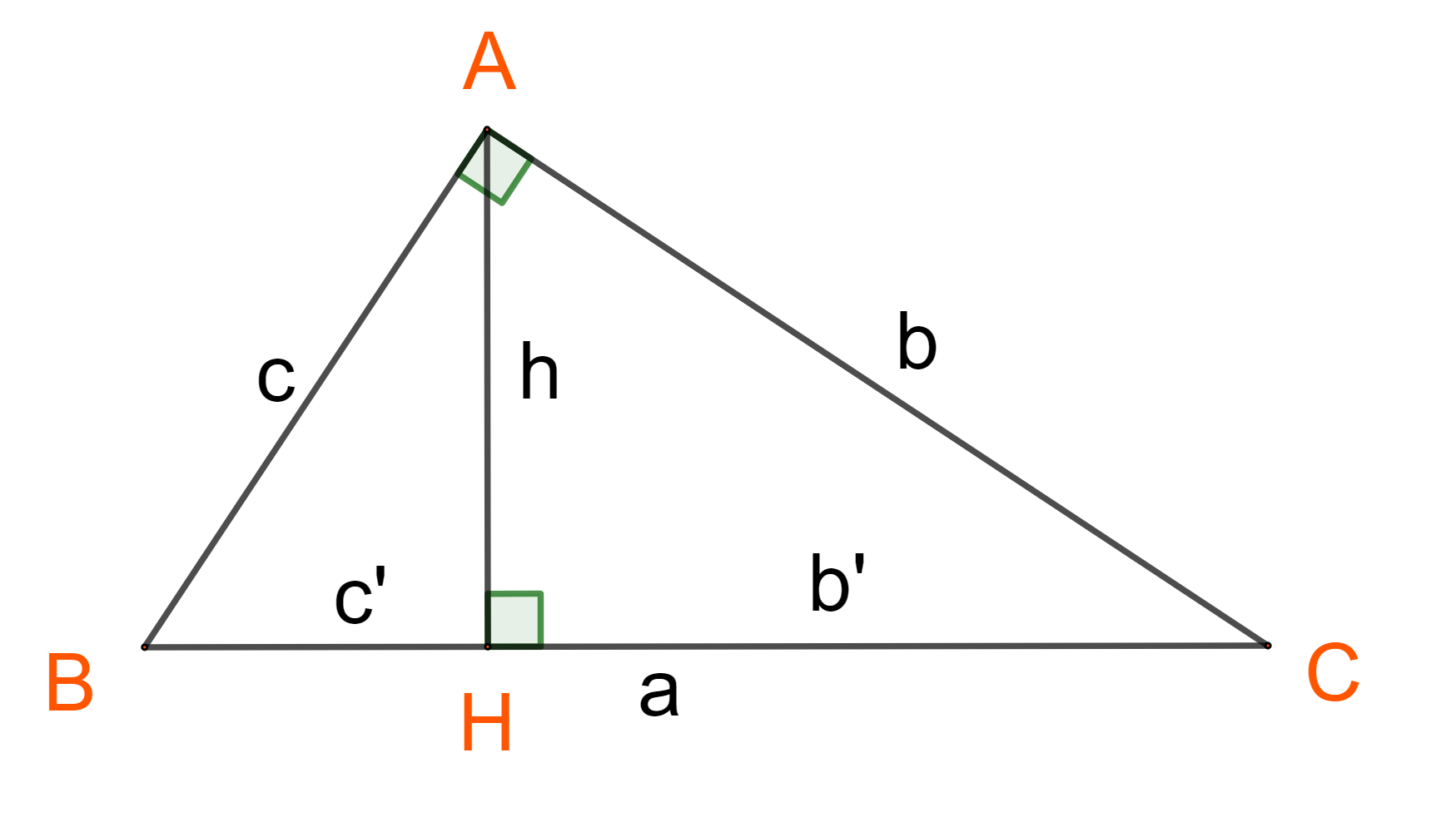
Trong đề bài ta có một hình tam giác vuông ABC và dữ liệu được cho sẵn là vuông tại A cùng với AH là đường cao của tam giác này, khi đó ta có các hệ thức mà các bạn học sinh lớp 9 cần nhớ liên quan sau đây:

Các hệ thức liên quan đến hệ thức lượng trong tam giác vuông và tam giác thường

AB bình = BH * BC
AC bình = CH * BC
AH bình = BH * CH
AB * AC = AH * BC
1/đường cao bình = 1/AB bình * 1/AC bình
Cạnh huyền trong tam giác bình phương bằng tổng bình phương của hai cạnh góc vuông trong tam giác đó.
Tỉ số lượng giác của góc nhọn
Một số kiến thức quan trọng có liên quan đến các công thức lượng giác và hệ thức lượng tam giác vuông mà chúng tôi chuẩn bị nhắc tới như sau:

a) Định nghĩa về tỉ số lượng giác

Sin alpha = Đối / Huyền
Cos alpha = Kề / Huyền
Tan alpha = Đối / Kề
Cot alpha = Kề / Đối
b) Định lý về tỷ số lượng giác

Trong một tam giác vuông được cho sẵn , nếu hai góc phụ nhau thì có công thức áp dụng giải bài tập như: sin góc này bằng cos góc kia, tan góc này bằng cot góc kia và ngược lại.

c) Các so sánh cần nhớ của hệ số lượng giác

Nắm vững kiến thức để làm bài dễ dàng hơn

 

Cho 2 góc alpha và belta được nhận diện là 2 góc nhọn của một tam giác vuông tức là hai góc có tổng số đo là 90 độ và alpha bé hơn belta thì:

Sin alpha < Sin beta và đồng thời Tan alpha < Tan beta
Cos alpha > Cos beta và tương tự ta có Cot alpha > Cot beta
Sin alpha < Tan alpha và bên cạnh đó thì Cos alpha < Cot alpha

Ứng dụng tam giác trong xây dựng

2. Ứng dụng của hệ thức lượng trong tam giác vuông

Hệ thức lượng trong tam giác vuông không chỉ là công cụ quan trọng trong toán học mà còn có nhiều ứng dụng thực tiễn trong các lĩnh vực khác nhau. Dưới đây là một số ứng dụng phổ biến của các hệ thức lượng giác trong tam giác vuông:

Tính Toán Các Đoạn Đo Trong Tam Giác Vuông
Tính Chiều Cao và Độ Dài Các Cạnh:
Công thức: Sử dụng các hệ thức lượng giác như
sin cos, và tan
⁡
tan để tính chiều cao, độ dài của các cạnh còn lại khi biết một số cạnh và góc trong tam giác vuông.
Ví dụ: Nếu bạn biết một cạnh và góc trong tam giác vuông, bạn có thể tính các cạnh còn lại bằng công thức
sin,cos, hoặctan
⁡
Giải Các Bài Toán Về Đo Đạc
Đo Đạc Vị Trí:
Công thức: Các hệ thức lượng giác có thể giúp tính toán khoảng cách giữa hai điểm khi có một số thông tin về góc và khoảng cách.
Ví dụ: Trong khảo sát đất đai, đo đạc vị trí, và công trình xây dựng, các hệ thức lượng giác được sử dụng để xác định khoảng cách giữa các điểm không thể đo trực tiếp.
Xây Dựng và Kiểm Tra Các Cấu Trúc Xây Dựng
Kiểm Tra Góc và Đo Đạc:
Công thức: Dùng để kiểm tra và xác định các góc và độ dài trong quá trình thiết kế và xây dựng.
Ví dụ: Khi xây dựng một tòa nhà, bạn có thể sử dụng hệ thức lượng giác để đảm bảo các góc và cạnh đúng như thiết kế.
Tính Toán Vị Trí và Hướng Trong Định Vị GPS
Định Vị GPS:
Công thức: Hệ thức lượng giác được sử dụng trong các thuật toán GPS để xác định vị trí chính xác trên bề mặt trái đất.
Ví dụ: Trong hệ thống GPS, các phương trình lượng giác giúp xác định vị trí của các vệ tinh và khoảng cách từ các vệ tinh đến thiết bị của bạn.
Đồ Họa Máy Tính:
Công thức: Sử dụng để xác định các góc, khoảng cách và các phép biến đổi hình học trong thiết kế đồ họa và phát triển game.
Ví dụ: Trong các trò chơi video, hệ thức lượng giác giúp tạo ra chuyển động và hiệu ứng hình ảnh chính xác.
Tính Toán Vận Tốc và Chuyển Động
Chuyển Động Vật Lý:
Công thức: Các hệ thức lượng giác giúp tính toán vận tốc, gia tốc và chuyển động của các vật thể.
Ví dụ: Trong cơ học và vật lý, các hệ thức lượng giác được sử dụng để phân tích các chuyển động theo hướng và vận tốc trong các bài toán chuyển động.
Giải Quyết Các Bài Toán Trong Vật Lý
Cân Bằng Lực:
Công thức: Các hệ thức lượng giác giúp phân tích và cân bằng các lực trong bài toán vật lý.
Ví dụ: Trong phân tích lực trong cơ học, bạn có thể sử dụng các công thức lượng giác để xác định các thành phần của lực theo các hướng khác nhau.
Giải Quyết Các Bài Toán Trong Điện Lực
Phân Tích Mạch Điện:
Công thức: Dùng để phân tích và tính toán các thành phần của sóng điện và điện áp.
Ví dụ: Trong kỹ thuật điện, các hệ thức lượng giác được sử dụng để tính toán các pha và biên độ của sóng điện áp và dòng điện.

Hệ thức lượng giác trong tam giác vuông không chỉ có vai trò quan trọng trong các bài toán toán học mà còn được áp dụng rộng rãi trong các lĩnh vực kỹ thuật, xây dựng, khoa học, và công nghệ. Hiểu và ứng dụng các hệ thức này giúp giải quyết nhiều bài toán thực tiễn và nâng cao khả năng phân tích và tính toán trong các tình huống thực tế.

Các cạnh trong tam giác vuông

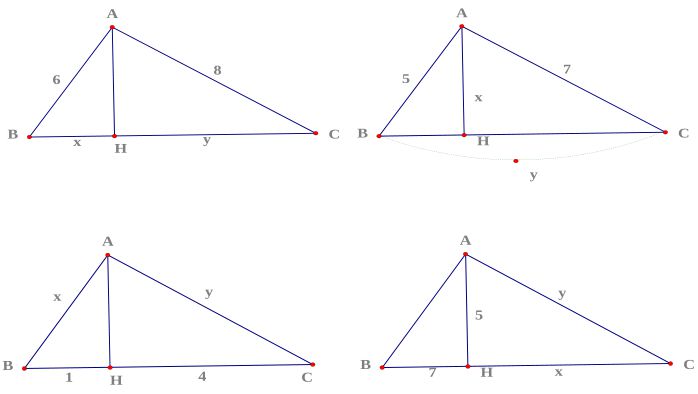
3. Bài ôn tập về hệ thức lượng trong tam giác vuông

Bài 26. Cho tam giác ABC có AB = 21m, AC = 28m, BC = 35m.

a) Chứng minh tam giác ABC vuông.

b) Tính sin B, sin C.

Bài 27. Cho tam giác ABC vuông tại A, đường cao AH, đường phân giác AD. Cho biết HB = 112, HC = 63.

a) Tính độ dài AH. b) Tính độ dài AD.

Bài 28. Cho tam giác ABC vuông tại A, đường cao AH. Biết AH = 5, CH = 6.

a) Tính AB, AC, BC, B b) Tính diện tích tam giác ABC.

Bài 29. Cho tam giác ABC vuông tại A, đường cao AH. Biết AH = 16, BH = 25.

a) Tính AB, AC, BC, CH. b) Tính diện tích tam giác ABC.

Bài 30. Cho hình thang ABCD có và hai đường chéo vuông góc với nhau tại O.

a) Chứng minh hình thang này có chiều cao bằng trung bình nhân của hai đáy.

b) Cho AB = 9, CD = 16. Tính diện tích hình thang ABCD.

c) Tính độ dài các đoạn thẳng OA, OB, OC, OD.

Bài 31. Tính diện tích hình thang ABCD (AB // CD), biết AB = 10, CD = 27, AC = 12, BD = 35.

Bài 32. Cho biết chu vi của một tam giác bằng 120cm. Độ dài các cạnh tỉ lệ với 8, 15, 17.

a) Chứng minh rằng tam giác đó là một tam giác vuông.

b) Tính khoảng cách từ giao điểm ba đường phân giác đến mỗi cạnh.

HD: Gọi O là giao điểm ba đường phân giác. Diện tích tam giác ABC = Diện tích tam giác OBC + Diện tích tam giác OCA + Diện tích tam giác OAB.

Các cạnh trong tác giác vuông

Bài 33. Cho tam giác ABC cân tại A, đường cao AH. Biết A = 48°, AH = 13cm. Tính chu vi tam giác ABC.

Bài 34. Cho tam giác ABC vuông tại A, AB = a, AC = 3a. Trên cạnh AC lấy các điểm D, E sao cho AD = DE = EC.

a) Chứng minh DE/DB = DB/DC.

b) Chứng minh tam giác BDE đồng dạng với tam giác CDB.

c) Tính tổng AFB + BCD.

Hy vọng rằng bài viết về Hệ thức lượng trong tam giác vuông lớp 9 ở trên sẽ giúp các em nắm chắc lý thuyết, cách làm bài tập về hệ thức lượng trong tam giác vuông cũng như đạt điểm cao hơn trong các bài thi, bài kiểm tra môn Toán.

Đừng quên tham khảo thêm 2 cuốn Làm chủ kiến thức Toán 9 ôn thi vào 10 phần Đại số và Hình học để biết cách giải tất cả các bài toán trong chương trình lớp 9 nhé!