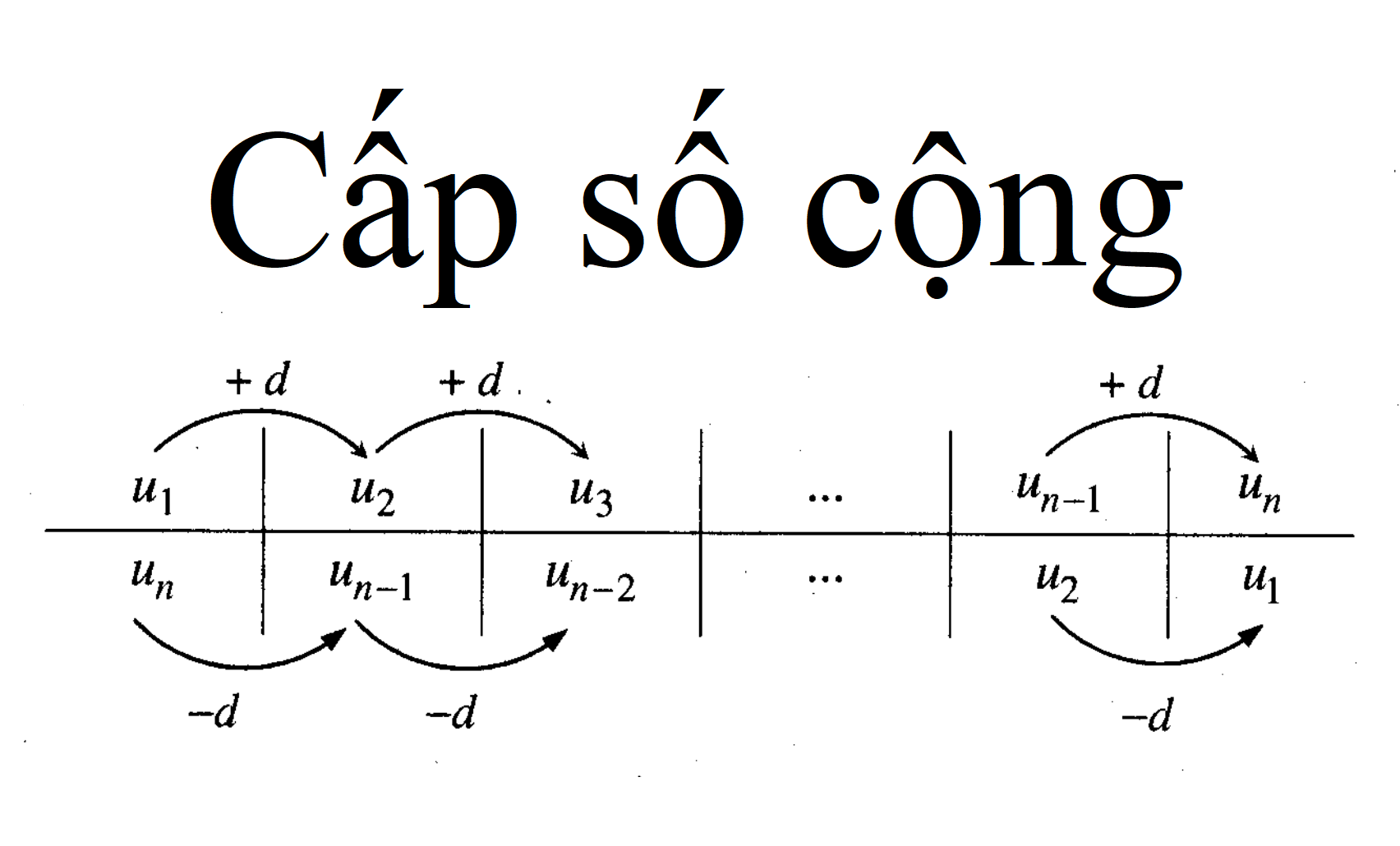Cấp Số Cộng Là Gì? Công Thức Cấp Số Cộng Và Bài Tập

1. Định nghĩa cấp số cộng

Cấp số cộng là một dãy số trong đó mỗi số hạng sau được tạo ra bằng cách cộng một giá trị không đổi vào số hạng trước đó. Giá trị không đổi này được gọi là công sai.

Đặc Điểm Chính
Công Sai (d):

Là giá trị không đổi được cộng vào mỗi số hạng để có số hạng kế tiếp. Ví dụ, nếu công sai là 3, thì mỗi số hạng tiếp theo trong dãy số sẽ lớn hơn số hạng trước đó 3 đơn vị.
Số Hạng Đầu:

Là số đầu tiên của dãy số. Ví dụ, trong dãy số 2,5,8,11, số hạng đầu tiên là 2.
Tính Chất:

Dãy số có tính chất rằng khoảng cách giữa bất kỳ hai số hạng liên tiếp là bằng nhau. Đây là đặc điểm chính của cấp số cộng.
Ví Dụ
Ví dụ 1: Dãy số 4,7,10,13,16 là một cấp số cộng.

Số hạng đầu tiên là 4.
Công sai là 3, vì mỗi số hạng sau được tạo ra bằng cách cộng thêm 3 vào số hạng trước.
Ví dụ 2: Dãy số 10,15,20,25 là một cấp số cộng.

Số hạng đầu tiên là 10.
Công sai là 5, vì mỗi số hạng sau được tạo ra bằng cách cộng thêm 5 vào số hạng trước.
Ứng Dụng
Tính Toán Đơn Giản: Cấp số cộng được sử dụng để mô tả các dãy số có sự tăng trưởng hoặc giảm sút đều đặn.
Tính Toán Tài Chính: Được sử dụng trong các tình huống như tính lãi suất hoặc các khoản thanh toán định kỳ.
Kết Luận
Cấp số cộng là một khái niệm toán học đơn giản nhưng quan trọng, giúp mô tả và giải quyết các vấn đề liên quan đến dãy số có sự gia tăng hoặc suy giảm đều đặn.

>>Tham khảo: Hằng đẳng thức bậc 3

Định nghĩa cấp số cộng trong toán học

2. Tính chất cấp số cộng

Cấp số cộng là một dãy số trong đó hiệu số giữa bất kỳ hai số hạng liên tiếp là một giá trị không đổi gọi là công sai. Dưới đây là các tính chất cơ bản của công thức cấp số cộng

 Hiệu Số Giữa Các Số Hạng Liên Tiếp
Tính Chất Đồng Nhất: Hiệu số giữa bất kỳ hai số hạng liên tiếp trong dãy cấp số cộng luôn là một giá trị không đổi. Nếu bạn lấy bất kỳ hai số hạng liên tiếp trong dãy và trừ số hạng trước đó khỏi số hạng sau, bạn sẽ luôn nhận được cùng một kết quả.
Tính Đồng Đều
Khoảng Cách Đều Đặn: Các số hạng trong công thức cấp số cộng phân bố đều nhau trên trục số. Điều này có nghĩa là sự khác biệt giữa bất kỳ hai số hạng liên tiếp là bằng nhau.
Dãy Số Cộng Đều
Sự Tăng Trưởng Hoặc Giảm Đều: Cấp số cộng có thể là dãy số đang tăng dần hoặc giảm dần. Nếu công sai là số dương, dãy số sẽ tăng; nếu công sai là số âm, dãy số sẽ giảm.
Số Hạng Trung Bình
Trung Bình Cộng: Trong cấp số cộng, số hạng ở giữa của dãy số (khi số hạng là số lẻ) luôn bằng trung bình cộng của số hạng đầu tiên và số hạng cuối cùng. Ví dụ, trong dãy số có 5 số hạng, số hạng thứ 3 sẽ là trung bình cộng của số hạng thứ 1 và số hạng thứ 5.
Đối Xứng
Tính Đối Xứng: Các số hạng trong dãy cấp số cộng có thể được chia thành các cặp đối xứng quanh số hạng giữa của dãy. Điều này có nghĩa là sự khác biệt giữa các số hạng đối xứng là bằng nhau.
Tính Tăng Trưởng Hoặc Suy Giảm Đều
Tăng Trưởng Hoặc Suy Giảm Đều: Cấp số cộng có thể được dùng để mô tả các hiện tượng trong đó sự thay đổi diễn ra đều đặn theo một tỷ lệ không đổi. Ví dụ, trong một kế hoạch tiết kiệm, số tiền tiết kiệm có thể tăng đều đặn mỗi tháng.

Ví Dụ 1: Dãy số 3,6,9,12,15 có hiệu số giữa các số hạng liên tiếp là 3. Đây là một cấp số cộng với công sai là 3, và các số hạng đều phân bố đều trên trục số.
Ví Dụ 2: Dãy số 20,15,10,5,0 có hiệu số giữa các số hạng liên tiếp là -5. Đây là một cấp số cộng giảm dần, và các số hạng cũng phân bố đều nhau.

Cấp số cộng có những tính chất cơ bản như hiệu số đều giữa các số hạng liên tiếp, sự phân bố đồng đều, và tính đối xứng trong dãy số. Hiểu rõ các tính chất này giúp nhận diện và làm việc với các dãy số có sự thay đổi đều đặn trong toán học và ứng dụng thực tiễn.

Công thức cơ bản của cấp số cộng

3. Công thức tính số hạng tổng quát của cấp số cộng

Các công thức Cấp số cộng
Công thức cấp số cộng theo định nghĩa chung
Un = Un-1 + d (n ≥ 2)

Un là số hạng thứ n
d là công sai
 Công thức tính số hạng tổng quát của cấp số cộng
Un = U1 + d(n – 1)

Un là số hạng thứ n
U1 là số hạng đầu tiên
d là công sai
n là số thứ tự của số hạng
 Công thức tính tổng n số hạng đầu tiên của cấp số cộng
Công thức tính tổng n số hạng đầu (tổng riêng thứ n) thông qua số hạng đầu và số hạng thứ n
Sn = U1 + U2 + … + Un = n(U1+Un)/2 (n ≥ 1)

Công thức tính tổng n số hạng đầu (tổng riêng thứ n) thông qua số hạng đầu và công sai
Sn = nU1+ [n(n-1)/2)]d (n ≥ 2)

Sn là tổng n số hạng đầu tiên
U1 là số hạng đầu tiên
d là công sai
n là số thứ tự của số hạng
Công thức tính số hạng đầu tiên
U1 = Sn – n/2(n – 1)d

U1 là số hạng đầu tiên
Sn là tổng n số hạng đầu tiên
d là công sai
n là số thứ tự của số hạng
Công thức tính công sai
d = Un – Un-1

d là công sai
Un là số hạng thứ n
U(n-1) là số hạng thứ n – 1
Công thức tính số hạng giữa
Um = (U1 + Un)/2

Um là số hạng giữa
U1 là số hạng đầu tiên
Un là số hạng thứ n

4. Kinh nghiệm làm bài tập về công thức cấp số cộng

Làm bài tập về công thức cấp số cộng có thể trở nên dễ dàng hơn nếu bạn nắm vững các kiến thức cơ bản và áp dụng các mẹo học tập hiệu quả. Dưới đây là một số kinh nghiệm giúp bạn giải bài tập cấp số cộng một cách hiệu quả:

Hiểu Khái Niệm Cơ Bản
Cấp Số Cộng: Là dãy số trong đó hiệu số giữa bất kỳ hai số hạng liên tiếp là một giá trị không đổi gọi là công sai.
Công Sai: Là sự khác biệt giữa các số hạng liên tiếp trong cấp số cộng.
Số Hạng Tổng Quát: Được tính bằng cách cộng số hạng đầu tiên với công sai nhân với chỉ số của số hạng đó trừ 1.
Xác Định Các Thông Tin Cần Thiết
Tìm Công Sai: Nếu bạn có hai số hạng liên tiếp, công sai là hiệu số giữa chúng.
Số Hạng Đầu Tiên: Xác định số hạng đầu tiên của dãy.
Chỉ Số Số Hạng: Xác định số thứ tự của số hạng mà bạn cần tính.

Nắm chắc kiến thức cơ bản trên lớp

Làm Nhiều Bài Tập Thực Hành
Thực Hành Đều Đặn: Làm nhiều bài tập khác nhau để làm quen với các loại bài tập cấp số cộng. Điều này giúp bạn nhanh chóng nhận diện các dạng bài tập và áp dụng các công thức một cách chính xác.
Sử Dụng Các Tài Nguyên Học Tập
Sách Giáo Khoa và Sách Bài Tập: Sử dụng các tài liệu học tập để giải bài tập và ôn tập kiến thức.
Ứng Dụng Học Tập: Sử dụng các ứng dụng học tập và phần mềm toán học để giải bài tập và kiểm tra kết quả.
Kiểm Tra và Xem Lại
Kiểm Tra Kết Quả: Luôn kiểm tra kết quả của bạn để đảm bảo tính chính xác. So sánh kết quả với các bài tập mẫu hoặc sử dụng phần mềm toán học để xác nhận.
Kết Luận
Việc làm bài tập cấp số cộng trở nên dễ dàng hơn khi bạn hiểu rõ khái niệm cơ bản, sử dụng các công thức chính xác, và thực hành thường xuyên. Bằng cách áp dụng các mẹo và phương pháp trên, bạn sẽ cải thiện khả năng giải bài tập và nắm vững kiến thức về cấp số cộng.

>> Tham khảo: Sơn dulux inspire nội thất