Số Nguyên Là Gì? Khái Niệm, Tính Chất Và Bài Tập Minh Họa

Số nguyên là gì?

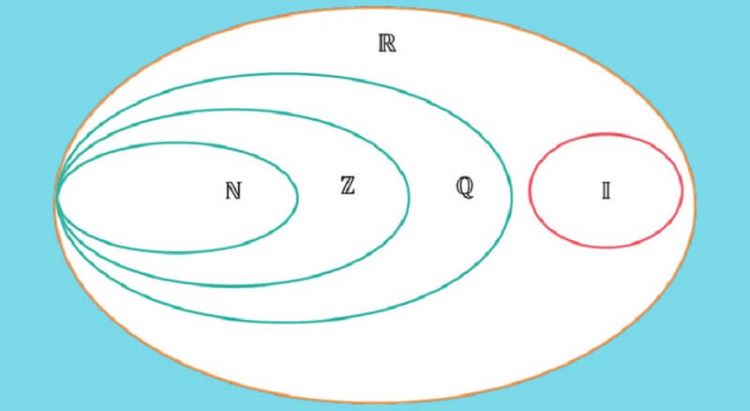
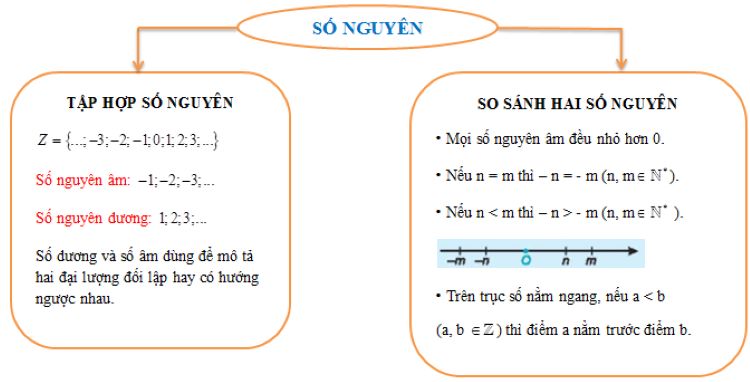
Trong toán học, số nguyên là tập hợp các số bao gồm:

Số nguyên dương: 1, 2, 3, 4, …

Số nguyên âm: -1, -2, -3, -4, …

Số 0

Tập hợp số nguyên được ký hiệu là Z.

Nói cách khác, số nguyên là tập hợp các số không có phần thập phân hay phân số. Ví dụ: -5, 0, 12 đều là số nguyên, trong khi 3,5 hoặc 7/2 không phải số nguyên.

 

Trong chương trình toán học lớp 6, khái niệm số nguyên là một trong những nền tảng quan trọng, giúp học sinh mở rộng phạm vi số từ số tự nhiên sang những con số âm. Đây cũng là cơ sở để học các phần kiến thức cao hơn như số hữu tỉ, số thực, phương trình, bất phương trình.

Tính chất cơ bản của số nguyên là gì?

Tập hợp số nguyên có nhiều tính chất quan trọng, thường gặp trong chương trình toán học phổ thông. Một số tính chất tiêu biểu:

Tính chất cộng

Tổng của hai số nguyên bất kỳ luôn là một số nguyên.

Ví dụ: 5 + (-3) = 2; (-4) + (-7) = -11.

Phép cộng có tính chất giao hoán: a + b = b + a.

Phép cộng có tính chất kết hợp: (a + b) + c = a + (b + c).

Tính chất trừ

Hiệu của hai số nguyên bất kỳ cũng luôn là một số nguyên.

Ví dụ: 7 – 10 = -3.

Tính chất nhân

Tích của hai số nguyên bất kỳ là một số nguyên.

Ví dụ: (-3) × 4 = -12.

Phép nhân có tính chất giao hoán và kết hợp.

Quy tắc dấu:

(+) × (+) = (+)

(-) × (-) = (+)

(+) × (-) = (-)

Tính chất chia

Không phải mọi số nguyên đều chia hết cho nhau. Ví dụ: 7 chia cho 3 không cho kết quả là số nguyên.

Tính chất đối

Mỗi số nguyên a luôn có số đối -a, sao cho a + (-a) = 0.

Tính chất so sánh

Trong tập hợp số nguyên:

Các số dương lớn hơn 0.

Các số âm nhỏ hơn 0.

Số 0 đứng giữa số nguyên âm và dương.

Những tính chất này là cơ sở cho nhiều dạng toán: cộng trừ nhân chia số nguyên, giải phương trình, bất đẳng thức…

Biểu diễn số nguyên trên trục số

Để dễ dàng hình dung, ta thường biểu diễn số nguyên trên trục số.

Trục số là một đường thẳng:

Chọn một điểm làm gốc O (ứng với số 0).

Chọn một đơn vị đo.

Các số nguyên dương nằm về phía bên phải O.

Các số nguyên âm nằm về phía bên trái O.

 

Ví dụ:

… -4, -3, -2, -1, 0, 1, 2, 3, 4 …

 

Khoảng cách từ O đến điểm biểu diễn số nguyên a chính là giá trị tuyệt đối của a, ký hiệu |a|.

Ví dụ: |3| = 3, |-5| = 5.

Trục số giúp chúng ta dễ dàng so sánh số nguyên, thực hiện phép tính cộng trừ bằng cách di chuyển sang phải hoặc sang trái.

Ví dụ

Tính 2+ (-5): từ vị trí số 2 trên trục số, lùi sang trái 5 đơn vị, ta đến -3.

Tính -4 + 7: từ vị trí -4, tiến sang phải 7 đơn vị, ta đến 3.

Ứng dụng của số nguyên trong thực tế

Số nguyên không chỉ là kiến thức lý thuyết mà còn có rất nhiều ứng dụng trong đời sống.

Trong nhiệt độ

Nhiệt độ dưới 0 độ C được biểu diễn bằng số nguyên âm. Ví dụ: -10°C.

Trong tài chính

Số dương thể hiện lợi nhuận.

Số âm thể hiện thua lỗ hoặc nợ.

Trong độ cao và độ sâu

Độ cao trên mực nước biển: số nguyên dương.

Độ sâu dưới mực nước biển: số nguyên âm.

 

Trong thể thao

Điểm số có thể tăng (dương) hoặc giảm (âm) tùy luật chơi.

Bảng xếp hạng thường dùng số nguyên để tính điểm.

 

Trong công nghệ thông tin

Số nguyên được dùng trong lập trình để xử lý dữ liệu, lưu trữ số liệu, xây dựng thuật toán.

 

Trong khoa học và kỹ thuật

Biểu diễn điện tích dương, điện tích âm.

Thể hiện dòng điện một chiều (+ và -).

Các phép đo vật lý thường quy đổi về số nguyên để thuận tiện tính toán.

Như vậy, số nguyên không chỉ tồn tại trong toán học mà còn gắn liền với nhiều khía cạnh của cuộc sống.

Bài tập minh họa về số nguyên là gì?

Để hiểu rõ hơn, ta cùng luyện tập một số bài tập cơ bản và nâng cao.

Bài tập 1: Tính các tổng sau:

1. a) 7 + (-3)
2. b) -8 + (-5)
3. c) -6 + 12

Lời giải:

1. a) 7 + (-3) = 4
2. b) -8 + (-5) = -13
3. c) -6 + 12 = 6

Bài tập 2: Thực hiện phép nhân và cho biết dấu của kết quả:

1. a) (-4) × 7
2. b) (-5) × (-2)
3. c) 9 × (-3)

Lời giải:

1. a) -28 (âm)
2. b) 10 (dương)
3. c) -27 (âm)

Bài tập 3: So sánh các số sau:

1. a) -7 và -3
2. b) 0 và -5
3. c) 8 và 12

Lời giải:

1. a) -7 < -3
2. b) 0 > -5
3. c) 8 < 12

Bài tập 4 (thực tế): Nhiệt độ buổi sáng là -5°C, buổi trưa tăng thêm 8°C. Hỏi nhiệt độ buổi trưa là bao nhiêu?

Lời giải:

-5 + 8 = 3°C.

Bài tập 5 (nâng cao): Một tàu ngầm đang ở độ sâu -120m. Nó nổi lên 75m rồi lại lặn xuống thêm 50m. Hỏi vị trí cuối cùng của tàu ngầm?

Lời giải:

Độ sâu cuối = -120 + 75 – 50 = -95m.

Qua bài viết, chúng ta đã cùng tìm hiểu về số nguyên: từ khái niệm, tính chất cơ bản của số nguyên, cách biểu diễn số nguyên trên trục số, đến ứng dụng số nguyên trong thực tế và các bài tập minh họa.

Số nguyên là gì nền tảng quan trọng trong toán học, đặc biệt ở cấp trung học cơ sở, đồng thời gắn liền với đời sống thực tế: nhiệt độ, tài chính, độ cao, kỹ thuật, khoa học. Việc nắm chắc số nguyên giúp học sinh dễ dàng tiếp thu các kiến thức cao hơn như số hữu tỉ, số thực, đại số và giải tích.