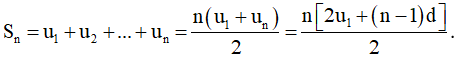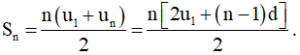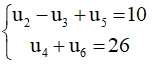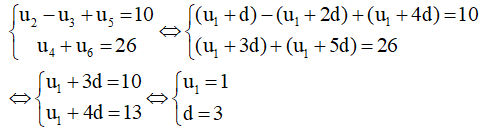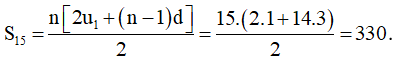Công Thức Cấp Số cộng, Cấp Số Nhân Và Bài Tập Liên Quan

Công thức cấp số cộng, cấp số nhân là kiến thức các em được học trong chương trình lớp 11. Do đó, đây là một nội dung quan trọng giúp các em đạt điểm cao trong kỳ thi lớp 11 và chuẩn bị hành trang cho thi tốt nghiệp.

1. Tổng quan về Cấp số nhân và Cấp số cộng

Cấp số nhân và cấp số cộng là 2 khái niệm cơ bản trong toán học. Thường áp dụng để mô hình hóa các dãy số và trong nhiều ứng dụng thực tế.

Cấp số nhân được hiểu là một chuỗi các số được tạo ra bằng cách nhân số trước đó với một hằng số cố định. Trong khi đó, cấp số cộng lại là một chuỗi các số được tạo ra bằng cách cộng với một hằng số cố định.

Hiểu và áp dụng đúng cách cả 2 khái niệm sẽ giúp chúng ta áp dụng một cách hiệu quả trong nhiều lĩnh vực, từ toán học đến kinh tế, khoa học xã hội và cả kỹ thuật.

>> Xem thêm: Hằng đẳng thức bậc 3

2. Cấp số cộng và công thức cấp số cộng

2.1 Định nghĩa

a) Định nghĩa: (un) là cấp số cộng khi un+1 = un + d, n ∈ N* (Trong đó d gọi là công sai)

Nhận xét:

– Cấp số cộng (un) là một dãy số tăng dần khi và chỉ khi công sai d > 0. 

– Cấp số cộng (un) là một dãy số giảm dần khi và chỉ khi công sai d < 0. 

– Đặc biệt, với d = 0 thì cấp số cộng là một dãy số không đổi (tất cả các số hạng đều sẽ bằng nhau). 

b) Số hạng tổng quát của cấp số cộng (un) được xác định bởi công thức cấp số cộng như sau:

un = u1 + (n – 1)d với n ∈ N*, n ≥ 2.

c) Tính chất:

Ba số hạng uk-1, uk, uk+1 (k ≥ 2) là ba số hạng liên tiếp của cấp số cộng khi và chỉ khi

d) Tổng n số hạng đầu tiên Sn sẽ được xác định bởi công thức:

2.2. Công thức cấp số cộng

– Công thức tính công sai: d = un+1 – un với n ∈ N*.

– Công thức tìm ra số hạng tổng quát: un = u1 + (n – 1)d với n ∈ N* và n ≥ 2. 

– Tính chất của 3 số hạng uk-1, uk, uk+11 (k ≥ 2) liên tiếp của cấp số cộng: 

– Tổng n số hạng đầu tiên của cấp số cộng được tính bằng: 

2.3. Ví dụ áp dụng công thức cấp số cộng

Ví dụ 1: Cho cấp số cộng (un) thỏa mãn: 

a) Xác định công sai và số hạng đầu tiên của cấp số cộng trên.

b) Xác định công thức số hạng tổng quát của cấp số cộng này.

c) Tính số hạng thứ 100 của cấp số cộng. 

d) Tính ra tổng 15 số hạng đầu tiên của cấp số cộng.

Lời giải

a) Gọi d là công sai của cấp số cộng, ta có: 

Vậy công sai d = 3 và số hạng đầu tiên u1 = 1. 

b) Số hạng tổng quát: un = u1 + (n – 1)d = 1 + (n – 1).3 = 3n – 2.

c) Số hạng thứ 100 là: u100 = 3.100 – 2 = 298.

d) Tổng 15 số hạng đầu tiên: 

Ví dụ 2: Cho cấp số cộng (un) thỏa mãn: un = 2n – 3.

a) Xác định công sai của cấp số cộng

b) Số 393 là số hạng thứ bao nhiêu của cấp số cộng trên?

c) Tính tổng S = u1 + u3 + u5 + … + u2021

Lời giải

a) Ta có: un+1= 2(n + 1) – 3 = 2n – 1

Công sai của cấp số cộng sẽ bằng: d = un+1 – un = (2n – 1) – (2n – 3) = 2

b) Gọi số hạng thứ k của cấp số cộng là 393, ta có uk = 393. 

Khi đó: 2k – 3 = 393.=> k = 198.

Vậy số 393 chính là số hạng thứ 198 của cấp số cộng.

c) Ta có: u1 = 2 . 1 – 3 = – 1

Dãy số là (vn): u1; u3; u5; … u2021 là cấp số cộng. Trong đó số hạng đầu tiên là u1 = – 1 và công sai d’ = u3 – u1 = 2d = 4

Dãy (vn) có: (2021 – 1) : 2 + 1 = 1011 số hạng

>> Tham khảo: Bảng giá sơn kova TPHCM

3. Cấp số nhân, công thức cấp số nhân

Định nghĩa: Cấp số nhân là một dãy số trong đó có số hạng đầu khác không và kể từ số hạng thứ hai đều bằng tích của số hạng đứng ngay trước nó với một số không đổi khác 0 và khác 1 , được gọi là công bội q.

Công thức tổng quát có dạng: Un+1=Un.q

Trong đó

n ∈ N*, Công bội là q

Hai số liên tiếp trong công bội  lần lượt là Un,Un+1

Tính chất như sau: 

Un+1/Un=Un+2/Un+1

Un+1=√(Un.Un+2) , Un > 0

Ta thấy: {Un+1=Un.q

un=u1.qn−1,(n≥2)⇒u2k=uk−1.uk+1,(n≥2)

+ Số hạng tổng quát: Un=U1.qn−1

+ Tổng n số hạng đầu tiên sẽ bằng: Sn=U1+U2+…+Un=U11−qn1−q

+ Tổng của cấp số nhân lùi vô hạn: Với |q| < 1 thì Sn=U1+U2+…+Un=U11−q

 

4. So sánh giữa công thức Cấp số nhân và Cấp số cộng

Cấp số nhân và cấp số cộng là hai khái niệm quan trọng trong toán học, đặc biệt là trong lĩnh vực đại số và phân tích. Dưới đây là 1 vài điểm khác biệt cơ bản giữa chúng:

Định nghĩa:

Cấp số nhân là một dãy số, Trong đó mỗi số sau đều nhân với một hằng số cố định để thu ra được số tiếp theo.

Cấp số cộng là một dãy số, trong đó mỗi số sau đều cộng với một hằng số cố định để thu ra được số tiếp theo.

Biểu diễn toán học:

Cấp số nhân được biểu diễn dưới dạng a, ar, ar², ar³, …, trong đó a chính là số hạng đầu tiên và r là hằng số nhân.

Cấp số cộng sẽ được biểu diễn bằng dạng a, a + d, a + 2d, a + 3d, …, trong đó a là số hạng đầu tiên và d chính là hằng số công.

Mối quan hệ giữa các số với nhau

Trong cấp số nhân, mỗi số đứng sau đều được tạo ra bằng cách nhân số trước đó với một hằng số cố định. Do đó giữa chúng có một mối quan hệ nhân quan đặc biệt giữa các số trong dãy.

Trong cấp số cộng, mỗi số sau được tạo ra bằng cách cộng với một hằng số cố định. Do vậy mà chúng cũng có một mối quan hệ cộng đơn giản giữa các số trong dãy.

Tính chất và ứng dụng:

Cấp số nhân thường dùng trong mô hình sự gia tăng hay giảm dần theo tỉ lệ nhất định. Chẳng hạn như bài toán tăng trưởng dân số, phân hủy hóa học, hoặc tính toán lãi suất lũy kế.

Trong khi đó, Cấp số cộng thường được áp dụng để mô tả các chuỗi có sự gia tăng hay giảm dần theo một đơn vị cố định. Chẳng hạn như trong tính toán về quãng đường di chuyển hàng ngày hay trong việc dự đoán mức độ tăng trưởng tài chính.

5. Ứng dụng của cấp số cộng và cấp số nhân trong thực tế

Cả cấp số nhân và cấp số cộng đều có những ứng dụng nhất định, từ các lĩnh vực khoa học cho đến tài chính và kinh doanh. Dưới đây là một vài ứng dụng phổ biến của chúng:

Ứng dụng của Cấp số nhân:

Tài chính: Trong lĩnh vực tài chính, cấp số nhân được áp dụng để tính toán lãi suất lũy kế và tỷ lệ tăng trưởng của các khoản đầu tư hay tài sản trong thời gian.

Khoa học: Trong nhiều lĩnh vực như sinh học và hóa học, cấp số nhân thường được sử dụng để mô hình sự tăng trưởng dân số, sự phân hủy hay sự phát triển của các loại vi sinh vật.

Công nghệ: Trong lĩnh vực công nghệ, cấp số nhân được dùng trong việc mô tả sự gia tăng hoặc giảm dần của các yếu tố. Như số lượng người dùng, dung lượng lưu trữ hay tốc độ xử lý.

Ứng dụng của Cấp số cộng:

Quản lý sản xuất: Trong sản xuất, cấp số cộng thường dùng để dự đoán và quản lý sản lượng, đặt mục tiêu sản xuất hay tính toán nhu cầu nguyên liệu và lao động theo thời gian thực.

Hoạt động kinh doanh: Trong kinh doanh, cấp số cộng có thể dùng trong tính toán doanh số bán hàng hàng tháng, lợi nhuận thu từ chiến dịch kinh doanh, chiến dịch quảng cáo, hay số lượng khách hàng mới trong một khoảng thời gian.

Giáo dục: Trong giáo dục, cấp số cộng dùng để tạo ra các bảng tính đơn giản, ví dụ như bảng cửu chương, để giúp cho học sinh học và nhớ các phép tính cơ bản.

6.Một số bài tập về cấp số cộng

Bài 1: Cho các dãy số sau, dãy số nào là cấp số cộng. Nếu là cấp số cộng hãy xác định số hạng đầu tiên và công sai của nó

a) – 2; 1; 4; 7; 10; 13; 16; 19.

b) 2; 4; 6; 10; 12; 14; 16; 18; 20.

c) Dãy số (an), với an = 4n – 3.

Lời giải

a) Ta có: 1 – (– 2) = 4 – 1 = 7 – 4 = 10 – 7 = 13 – 10 = 16 – 13 = 19 – 16 = 3

Do đó dãy số – 2; 1; 4; 7; 10; 13; 16; 19 là cấp số cộng.

Với Số hạng đầu tiên của cấp số cộng là u1 = – 2, công sai là d = 3.

b) Ta thấy: 4 – 2 = 2 nhưng 10 – 6 = 4

Do đó dãy số 2; 4; 6; 10; 12; 14; 16; 18; 20 không phải là cấp số cộng.

c) Ta có: an = 4n – 3 thì an+1 = 4(n + 1) – 3.

Xét an+1 – an = 4(n + 1) – 3 – (4n – 3) = 4 (số không đổi)

Do đó dãy số (an) với an = 4n – 3 là cấp số cộng.

Vậy Số hạng đầu tiên của cấp số cộng là a1 = 4.1 – 3 = 1, với công sai là d = 4.

 

Bài 2: Cho cấp số cộng (un) thỏa mãn: 

u2-u3+u5=10 và u4+u6=26

a) Xác định công sai d và số hạng đầu tiên của cấp số cộng trên.

b) Xác định công thức tổng quát của cấp số cộng trên.

c) Tìm số hạng thứ 10 của cấp số cộng trên.

d) Số 6061 là số hạng bao nhiêu của cấp số cộng.

Lời giải

Gọi cấp số cộng có số hạng đầu tiên là u1 và công sai d

Số hạng tổng quát của (un) là un = u1 + (n – 1)d

Ta có:

u2-u3+u5 = 10 <=> u1+d- (u1+2d)+ u1+ 4d=10 <=> u1+3d = 10 (1)

u4+ u6= 26 <=> u1+3d + u1+5d = 26 <=> 2u1 + 8d =26 (2)

Từ (1) và (2) , ta suy ra được: u1= 1 và d = 3

Vậy u1 = 1 và d = 3.

b) Số hạng tổng quát là: un = 1 + (n – 1).3 hay un = 3n – 2 với n >1

c) Số hạng thứ 10 của cấp số cộng: u15 = 3.10 – 2 = 28

d) Giả sử số hạng thứ k của cấp số cộng là uk = 6061, ta có: uk = 3k – 2 = 6061, suy ra k = 2021.

Vậy số 6061 là số hạng thứ 2021 của cấp số cộng.

Bài 3: 

a) Tìm x biết: x2 + 1, x – 2, 1 – 3x lập thành 1 cấp số cộng.

b) Cho cấp số cộng – 2, x, 6, y. Tính giá trị của biểu thức P = x2 + y2.

Lời giải

a) Ta có: x2 + 1, x – 2, 1 – 3x lập thành cấp số cộng

<=> x2 + 1 + 1- 3x = 2(x-2)

<=> x2- 5x+ 6= 0

=> x= 2 hoặc x= 3

Vậy x= 2 hoặc x= 3 là những giá trị cần tìm

b, Theo tính chất của cấp số cộng ta có: 

x= (-2+6)/ 2 = 2 

6 = (x+y)/2 => 6 =(2+y)/ 2 => y= 10

Vậy P= x2+y2= 22+ 102 = 104

 

Bài 4: Cho cấp số cộng (un)

a) (u­n) có số hạng tổng quát là: un = 7n – 3. Tính S100.

b) (u­n) có u2 + u22 = 40. Tính S23.

c) (u­n) có u4 + u8 + u12 + u16 = 224. Tính S19.

Lời giải

a) Từ công thức số hạng tổng quát, Ta có:

Số hạng đầu: u1 = 7 . 1 – 3 = 4;

Số hạng thứ hai là : u2 = 7 . 2 – 3 = 11;

Công sai: d = 11 – 4 = 7

Khi đó ta có:

S100= n[2u1+ (n-1)d]/2 = 100[2.4 +(100-1).7]/2 = 35050

b, Ta có: u2+u22= 40=> u1+ d + u1 + 21d= 40 <=> 2u1 + 22d = 40

Vậy S23 = 23 (2u1+22d)/2 = 23.40/ 2 = 460

c, Ta có: u4+u8+u12+ u16 = 224

<=> u1 + 3d + u1 + 7d + u1+ 11d + u1 + 15d = 224

<=> 4u1 + 36d = 224

<=> u1 + 9d = 56

vậy S19 = 19(2u1+18d)/2 = 19.(u1+9d)= 19.56= 1064