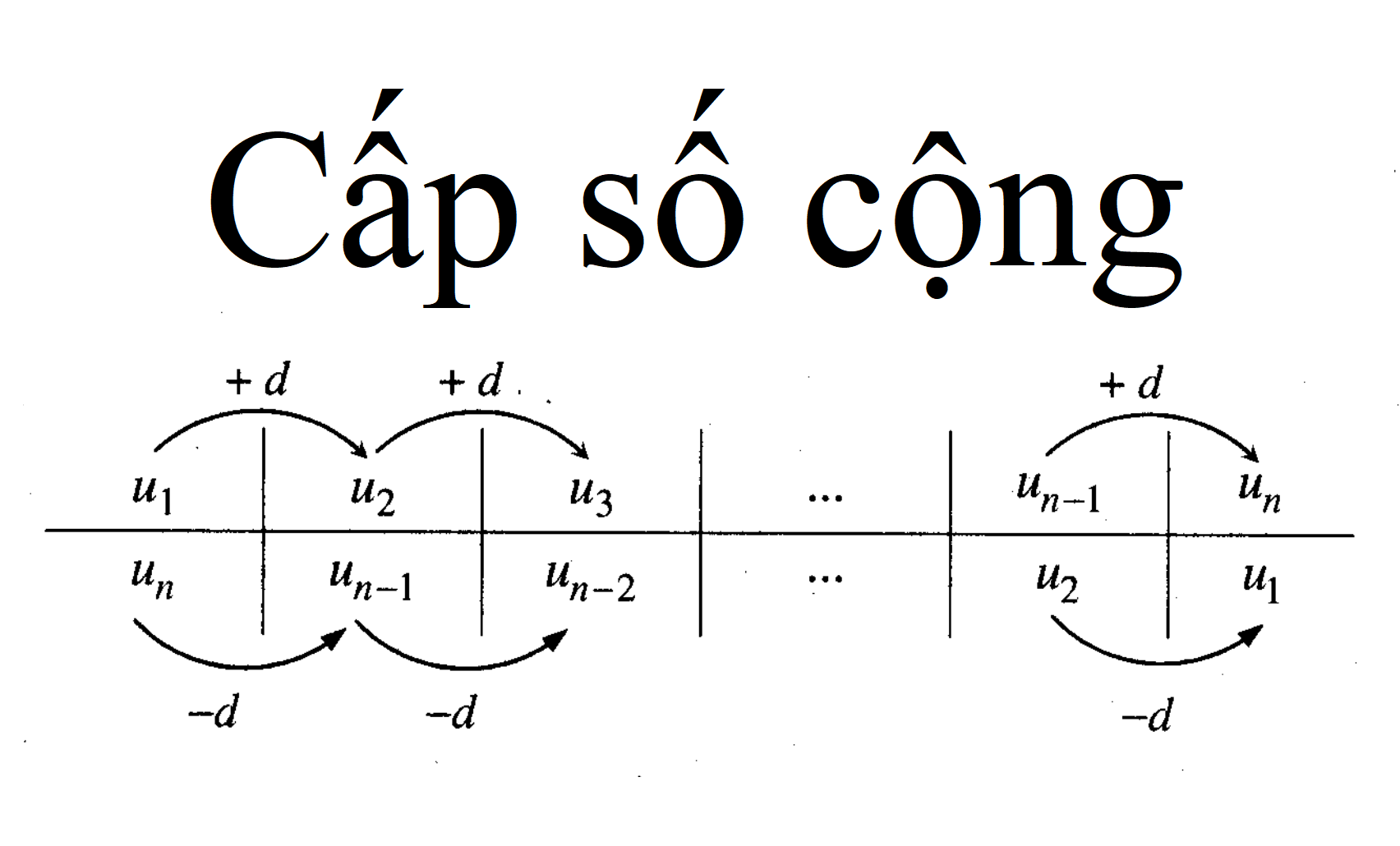Cấp số cộng là gì? Lý thuyết cấp số cộng và công thức cấp số cộng
1. Công thức cấp số cộng
Cấp số cộng là một dãy số mà mỗi số hạng sau cách số hạng trước một khoảng cách định. Khoảng cách này được gọi là công sai.
Ví dụ: 2, 4, 6, 8, 10 là một cấp số cộng với công sai là 2.
Công thức
Số hạng tổng quát
un=u1+d(n−1)
Trong đó:
un là số hạng thứ n
u1 là số hạng đầu tiên
d là công sai
n là vị trí của số hạng
Tổng n số hạng đầu tiên
Sn=n*(u_1+u_n)/2
Đặc điểm
Dễ dàng nhận biết: Nhìn vào dãy số, ta có thể thấy các số hạng tăng/giảm đều đặn theo một “công thức” nhất định.
Ứng dụng rộng rãi: Cấp số cộng xuất hiện trong nhiều lĩnh vực, từ khoa học tự nhiên đến khoa học xã hội, giúp mô tả các hiện tượng tăng trưởng/suy giảm theo thời gian.
Công cụ toán học hữu ích: Cấp số cộng được sử dụng để giải các bài toán liên quan đến tổng, trung bình, dãy số,…
>> Xem thêm: Hằng đẳng thức bậc 3
Ví dụ ứng dụng
Tính tổng số điểm thi của học sinh: Biết điểm của 3 học sinh đầu tiên lần lượt là 7, 8, 9. Ta có thể coi đây là 3 số hạng đầu tiên của một cấp số cộng để tính tổng điểm của cả lớp.
Mô phỏng sự tăng trưởng của vi khuẩn: Số lượng vi khuẩn sau mỗi giờ có thể được mô tả bằng một cấp số cộng, giúp dự đoán số lượng vi khuẩn trong tương lai.
Lập kế hoạch tiết kiệm: Ta có thể tính toán số tiền cần tiết kiệm mỗi tháng để đạt được mục tiêu tài chính trong một khoảng thời gian nhất định bằng cách sử dụng cấp số cộng.
Cấp số cộng
2. Tính chất công thức cấp số cộng
Tính chất
Hai số hạng liên tiếp hơn kém nhau một hằng số (công sai).
Có thể tăng hoặc giảm đều.
Số hạng tổng quát cho phép ta tính toán bất kỳ số hạng nào trong dãy số.
Công thức tổng n số hạng đầu tiên giúp tính tổng của một dãy số dài một cách nhanh chóng.
Ứng dụng
Cấp số cộng được ứng dụng rộng rãi trong nhiều lĩnh vực, bao gồm:
Toán học: tính tổng dãy số, giải phương trình, chứng minh định lý,…
Vật lý: tính quãng đường đi được, vận tốc,… trong chuyển động đều
Kinh tế: tính lãi suất kép, khấu hao tài sản,…
Khoa học máy tính: tối ưu hóa thuật toán, giải mã,…
Cấp số cộng
>> Tham khảo: Giá sơn chống thấm kova
3. Tổng n số hạng đầu tiên trong cấp số cộng
Công thức tính tổng n số hạng đầu tiên trong cấp số cộng là chìa khóa mở ra cánh cửa bí ẩn của dãy số. Nó cho phép ta tính toán tổng giá trị của n số hạng đầu tiên, hé lộ bức tranh toàn cảnh về sự tăng trưởng của cấp số cộng.
Công thức được viết dưới dạng:
Sn = n/2 * (2a1 + (n – 1)d)
Trong đó:
Sn: Tổng n số hạng đầu tiên
n: Số lượng số hạng cần tính tổng
a1: Số hạng đầu tiên của cấp số cộng
d: Công sai của cấp số cộng

Cấp số cộng
4. Các dạng toán thường gặp về cấp số cộng
Nhận biết cấp số cộng
Phương pháp:
Bước 1: Tính hiệu số của hai số hạng liên tiếp trong dãy.
Bước 2: Kết luận:
Nếu hiệu số của hai số hạng liên tiếp bằng nhau với mọi cặp số hạng liên tiếp trong dãy thì dãy là cấp số cộng.
Nếu hiệu số của hai số hạng liên tiếp khác nhau thì dãy không là cấp số cộng.
Ví dụ:
Dãy số 1, 3, 5, 7, 9:
Hiệu số giữa hai số hạng liên tiếp là 3 – 1 = 2 = 5 – 3 = 7 – 5 = 9 – 7 = 2.
Do hiệu số của hai số hạng liên tiếp bằng nhau nên dãy số 1, 3, 5, 7, 9 là cấp số cộng.
Tìm công sai của cấp số cộng
Phương pháp:
Sử dụng các tính chất của cấp số cộng, biến đổi để tìm công sai của cấp số cộng.
Ví dụ:
Dãy số 2, 5, 8, 11, … là cấp số cộng.
Ta có thể nhận biết dãy số này là cấp số cộng bằng cách tính hiệu số của hai số hạng liên tiếp: 5 – 2 = 3 = 8 – 5 = 11 – 8 = 3.
Để tìm công sai, ta có thể sử dụng phương trình:
u_{n + 1} = u_n + d
Với u_n là số hạng thứ n, u_{n + 1} là số hạng thứ n + 1 và d là công sai.
Thay u_n = 2 và u_{n + 1} = 5 vào phương trình trên, ta được:
5 = 2 + d
Giải phương trình, ta được d = 3.
Vậy công sai của cấp số cộng 2, 5, 8, 11, … là 3.
Tìm số hạng của cấp số cộng
Phương pháp:
Sử dụng công thức tính số hạng tổng quát:
u_n = u_1 + d(n – 1)
Với u_n là số hạng thứ n, u_1 là số hạng đầu, d là công sai và n là vị trí của số hạng trong dãy.
Ví dụ:
Tìm số hạng thứ 5 của cấp số cộng 3, 6, 9, 12, …
Số hạng đầu (u_1) là 3.
Công sai (d) là 3.
Vị trí của số hạng thứ 5 (n) là 5.
Thay các giá trị vào công thức, ta được:
u_5 = 3 + 3(5 – 1) = 15
Vậy số hạng thứ 5 của cấp số cộng 3, 6, 9, 12, … là 15.
Tính tổng n số hạng đầu tiên của dãy
Phương pháp:
Sử dụng công thức:
S_n = n/2 * [2u_1 + d(n – 1)]
Với S_n là tổng n số hạng đầu tiên, u_1 là số hạng đầu, d là công sai và n là số lượng số hạng cần tính tổng.
Ví dụ:
Tính tổng 10 số hạng đầu tiên của cấp số cộng 1, 4, 7, 10, …
Số hạng đầu (u_1) là 1.
Công sai (d) là 3.
Số lượng số hạng cần tính tổng (n) là 10.
Thay các giá trị vào công thức, ta được:
S_{10} = 10/2 * [2(1) + 3(10 – 1)] = 10/2 * [2 + 27] = 145
Vậy tổng 10 số hạng đầu tiên của cấp số cộng 1, 4, 7, 10, … là 145.
Trên đây là một số thông tin về công thức cấp số cộng. Hi vọng các bạn sẽ có cho mình thông tin thật sự hữu ích. Có một lưu ý nho nhỏ, các bạn hãy luyện tập thật nhiều để nắm thật chắc các công thức nhé!
Có thể bạn quan tâm:

Đại lý sơn nước chính hãng Thái Bình Dương
Chúng tôi luôn mong muốn mang đến giá trị cho cộng đồng chính là mang lại niềm tin trong tiêu dùng. Khách hàng có trải nghiệm mua sắm tuyệt vời. Hotline 0865.663.918 hoặc hòm thư: ngloan2712@gmail.com