Công Thức Cấp Số Cộng Đầy Đủ ? Bài Tập Áp Dụng

Trong chương trình đại số lớp 11, cấp số cộng là phần kiến thức quan trọng có tính ứng dụng cao. Bài viết dưới đây chúng tôi sẽ chia sẻ định nghĩa, công thức cấp số cộng và các dạng bài tập áp dụng.

1. Cấp số cộng là gì? Công thức cấp số cộng

Khái niệm: Cấp số cộng là 1 dãy số vô hạn hoặc hữu hạn trong đó các số hạng thỏa mãn điều kiện: kể từ số hạng thứ 2 trở đi, mỗi số hạng sẽ bằng số hạng đứng trước cộng với 1 số không đổi. Số hạng cộng không đổi đó gọi là công sai , được kí hiệu là d. 

Công thức cấp số cộng: Un = Un-1 + d

Trong đó: 

Un: cấp số cộng, d: công sai, n >= 2, n ∈ N*

Chẳng hạn: 

Dãy số tự nhiên 2,4,6,8,10…. là cấp số cộng với công sai d = 2

Dãy hằng số với các số hạng không đổi cũng là một cấp số cộng có công sai d = 0

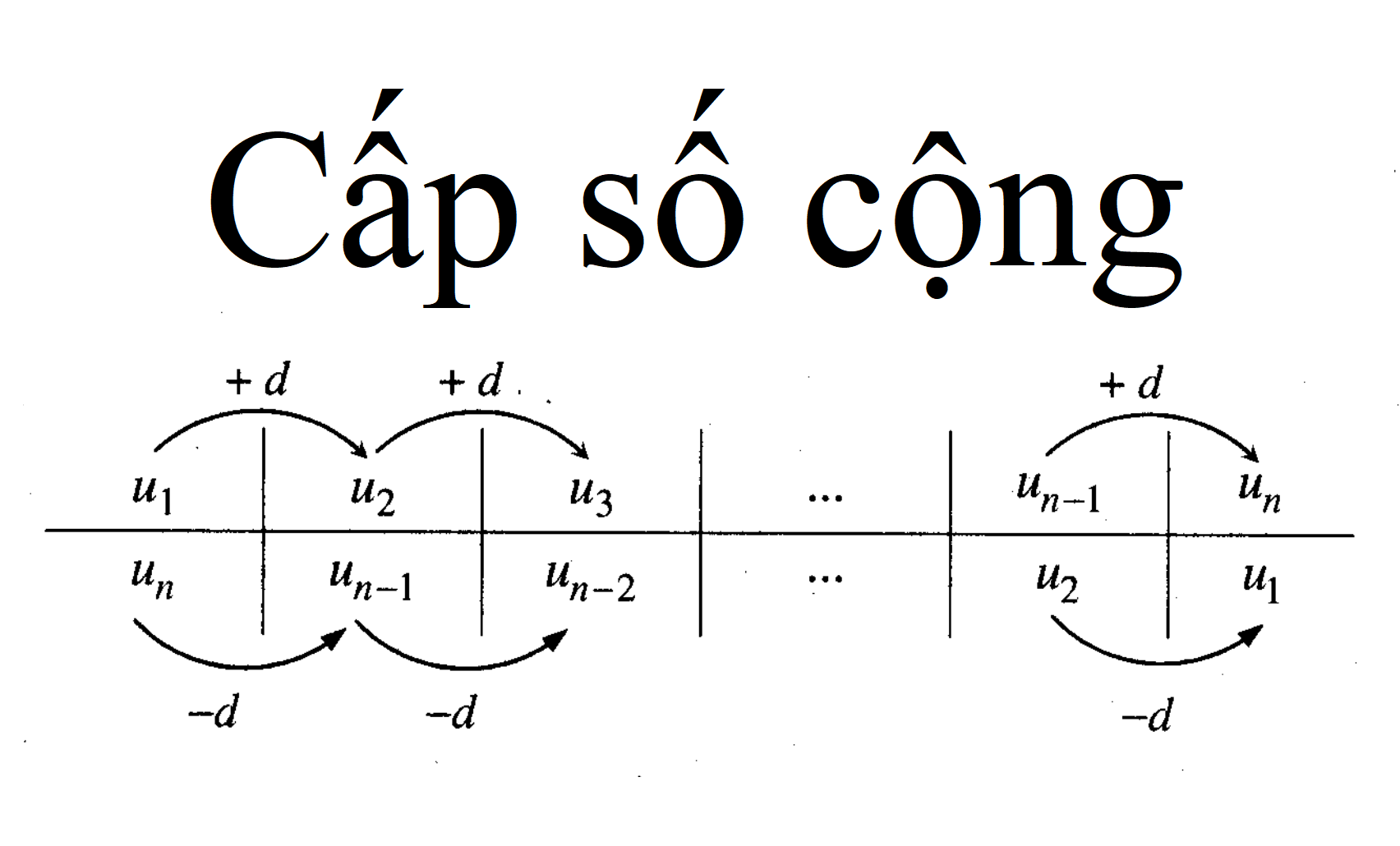
2. Tính chất của cấp số cộng

Bên cạnh đó thì Tính chất cấp số cộng lớp 11 cũng khá đặc biệt. Nếu Un là cấp số cộng thì kể từ số hạng thứ 2 đều sẽ là trung bình cộng của 2 số hạng đứng kế bên nhau trong dãy số. Trừ trường hợp số hạng cuối trong cấp số cộng là hữu hạn. 

Công thức như sau: Un = (Un-1 + Un+1) : 2

Chẳng hạn: 

Trong cấp số cộng có 3 số hạng liên tiếp lần lượt là 23, 26, 29

Thì Un = (23 + 29) : 2

=> Un = 26

Cách tính công sai cấp số cộng

Công thức tính công sai cấp số cộng có dạng tổng quát như sau: d = Un+1 – Un

Ví dụ: 

Cho cấp số cộng 2,6,10,14,18… Tính công sai cấp số cộng?

Lời giải:

Công sai với cấp số cộng là d = 6 – 2 = 10 – 6 = 14 – 10 = 18 – 14…= 4

3. Công thức số hạng tổng quát của một cấp số cộng

Nếu cấp số cộng có khởi đầu là phần tử U1, công sai cấp số cộng là d, thì số hạng thứ n (số hạng tổng quát) của cấp số cộng này có dạng tổng quát như sau: 

Công thức: Un = U1 + (n-1) d

Ví dụ: 

Cho cấp số cộng: 2,5,8,11,14… Biết dãy số của cấp số cộng trên có 9 số hạng, tìm số hạng thứ 9?

Lời giải

Công sai cấp số cộng trên d = 5 – 2 = 3

Áp dụng công thức số hạng tổng quát của cấp số cộng: Un = U1 + (n-1) d

=> Số hạng thứ 9 của cấp số cộng trên là: U9 = 2+ (9 – 1) 3

=> U9 = 26

Số hạng thứ 9 của cấp số cộng là 26

>> Xem thêm: Hằng đẳng thức bậc 3

4. Công thức tổng của cấp số cộng

 Dưới đây là công thứ tổng của cấp số cộng:

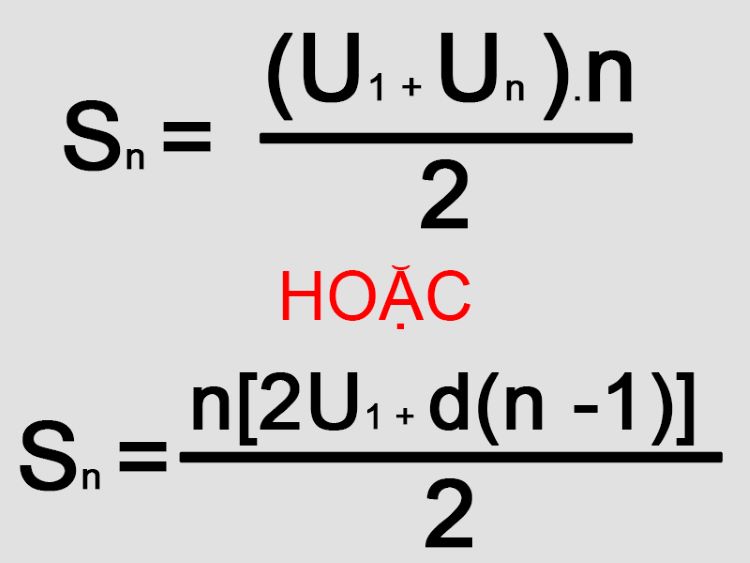
Công thức 1: Công thức tổng cấp số cộng của n số hạng đầu (tức tổng riêng thứ n) thông qua số hạng thứ n và số hạng đầu có dạng:

Sn = U1 + U2 + U3 +… + Un = n (U1 + Un) : 2

Trong đó: 

Sn: tổng cấp số cộng thứ n

Un: cấp số cộng

Công thức 2: Công thức tính tổng cấp số cộng của n số hạng đầu (tổng riêng thứ n) thông qua công sai d và số hạng đầu tiên: 

Sn = n . U1 + n (n-1) : 2 x d

Trong đó: 

Sn: tổng cấp số cộng

Un: cấp số cộng

d: công sai của cấp số cộng

5. Cách giải bài toán áp dụng công thức cấp số cộng

Từ các công thức về cấp số cộng trên, ta có thể áp dụng để giải các bài toán cấp số cộng một cách nhanh gọn và chính xác. Dưới đây chúng tôi sẽ giới thiệu các dạng bài điển hình nhé!

Dạng 1: Giải bài toán cấp số cộng vận dụng công thức cơ bản

Ví dụ 1: Cho dãy số 5, 10, 15, 20, 25. Đây có phải là cấp số cộng không? Tính công sai d nếu có? 

Đáp án: 

Dãy số 5, 10, 15, 20, 25 có công sai d là 

10 = 5 + 5

15 = 10 + 5

20 = 15 + 5

25 = 20 + 5

=> Do công sai d không đổi nên khẳng định dãy số 5, 10, 15, 20, 25 là cấp số cộng với công sai d = 5. Với số hạng đầu tiên U1 = 5 và số hạng cuối cùng U5 = 25

Dạng 2: Giải bài tập áp dụng công thức tìm số hạng tổng quát

Ví dụ 1: Cho cấp số cộng Un với U1 = 3, công sai d = 5. Tìm số hạng tổng quát của cấp số cộng trên?

Lời giải: 

Áp dụng công thức tìm số hạng tổng quát ta có

Un = U1 + (n – 1) d

=> Un = 3 + (n – 1) 3

=> Un = 3n 

Vậy số hạng tổng quát của cấp số cộng có U1 = 3, d = 5 là Un = 3n 

Dạng 3: Tìm ra số hạng bất kì của cấp số cộng

Bài tập: Tìm số hạng thứ 10 của cấp số cộng Un, cho biết số hạng thứ nhất U1 = 3, công sai d = 5. 

Lời giải

Áp dụng công thức tổng cấp số cộng của n số hạng đầu thông qua công sai d và số hạng đầu ta có:

Sn = n . U1 + n (n-1)/2 . d

=> S10 = 10 . 3 + 10 (10– 1)/2 . 5

=> S10 = 30 + 225

=> S10 = 255

Số hạng thứ 10 của cấp số cộng U10 trong đó có số hạng thứ nhất U1 =3, công sai d = 5 là U10 = 255

Dạng 4: Tính công sai của cấp số cộng

Ví dụ: Cho cấp số cộng có 25 số, với số hạng đầu tiên U1 = 3, tổng 25 số hạng đầu tiên là 1275. Tính công sai d của cấp số cộng?

Lời giải: 

Theo đề bài: S25 = 1275

Áp dụng công thức tính tổng cấp số cộng của n số hạng đầu (tổng riêng thứ n) thông qua số hạng thứ n và số hạng đầu ta có:

Sn = U1 + U2 + U3 +… + Un = n (U1 + Un)/2

=> S25 = 25 (U1 + U25)/2

<=> 1275 = 25 (3 + U25)/2

<=> 99 = U25

Áp dụng công thức ta có:

Sn = n . U1 + n (n-1)/2 . d

=> 1275 = 25 . 3 + 25 (25 – 1) : 2 . d

=>  1200 = 300 . d

=> d = 4

Vậy Công sai của cấp số cộng  trên d = 4

Dạng 5: Cho thông tin cấp số cộng, tính ra số hạng đầu của cấp số cộng

Ví dụ: Cho cấp số cộng Un thỏa mãn các điều kiện: U1 + U5 = 12 và U10 – U2 = 16. Tính số hạng đầu tiên của cấp số cộng Un.

Lời giải:

Theo đề bài ra ta có: 

U1 + U5 = 12

=> U1 + U1 + 4d = 12

=> U1 = 6 – 2d

U10 – U2 = 16

<=> 8d = 16

<=> d = 2

=> U1 = 6 – 2 . 2

=> U1 = 2

Vậy số hạng đầu tiên của cấp số cộng U1 = 1

Dạng 6: Áp dụng cấp số cộng vào bài toán thực tế

Ví dụ:

 Một nhà xưởng có chế độ đãi ngộ công nhân như sau: 

Lương quý đầu tiên của 1 công nhân là 12 triệu đồng/ quý

Lương từ quý thứ 2 sẽ tăng lên 1 triệu đồng/ quý

Vậy hãy tính lương của công nhân sau 5 năm làm việc tại đơn vị trên? 

Lời giải

Áp dụng công thức cấp số cộng ta có: 

Công nhân làm việc cho xưởng n quý

Quý đầu tiên là U1 = 12

Quý tiếp theo là Un+1 = Un + 1 (∀n ≥ 1)

Theo dữ liệu đề bài ra, lương mỗi quý là cấp số cộng Un trong đó lương quý sau sẽ hiều hơn quý trước là 1 triệu => Do đó công sai của cấp số cộng d = 1

Trong 1 năm có 4 quý nên 5 năm có 5 . 4 = 20 (quý)

=> Lương của công nhân sau 5 năm sau là  20 quý (U20). 

=> Lương tháng quý 20 của công nhân vận dụng công thức:

Un = U1 + (n – 1) d

<=> U20 = 12 + 19 x 1 = 21 ( triệu đồng)

Tổng lương công nhân nhận được sau 5 năm làm việc tại cơ sở là:

Sn = n . U1 + n (n-1)/ 2 . d

<=> S20 = 20 . 12 + 20 (20 – 1)/2 . 1

 

=> S20 = 430 (triệu đồng)

Vật Tổng lương công nhân nhận được sau 5 năm làm việc tại xưởng là 430 triệu đồng.

Trên đây là những kiến thức cơ bản về công thức cấp số cộng và các dạng bài liên quan. Hy vọng, các em áp dụng thành công và đạt điểm cao trong kỳ thi!

>> Tham khảo: Sơn chống thấm nippon