Hệ thức lượng trong tam giác vuông áp dụng cho các dạng bài toán nào.

Mục Lục

Hệ thức lượng trong tam giác vuông

1.Hệ thức lượng trong tam giác vuông là gì?

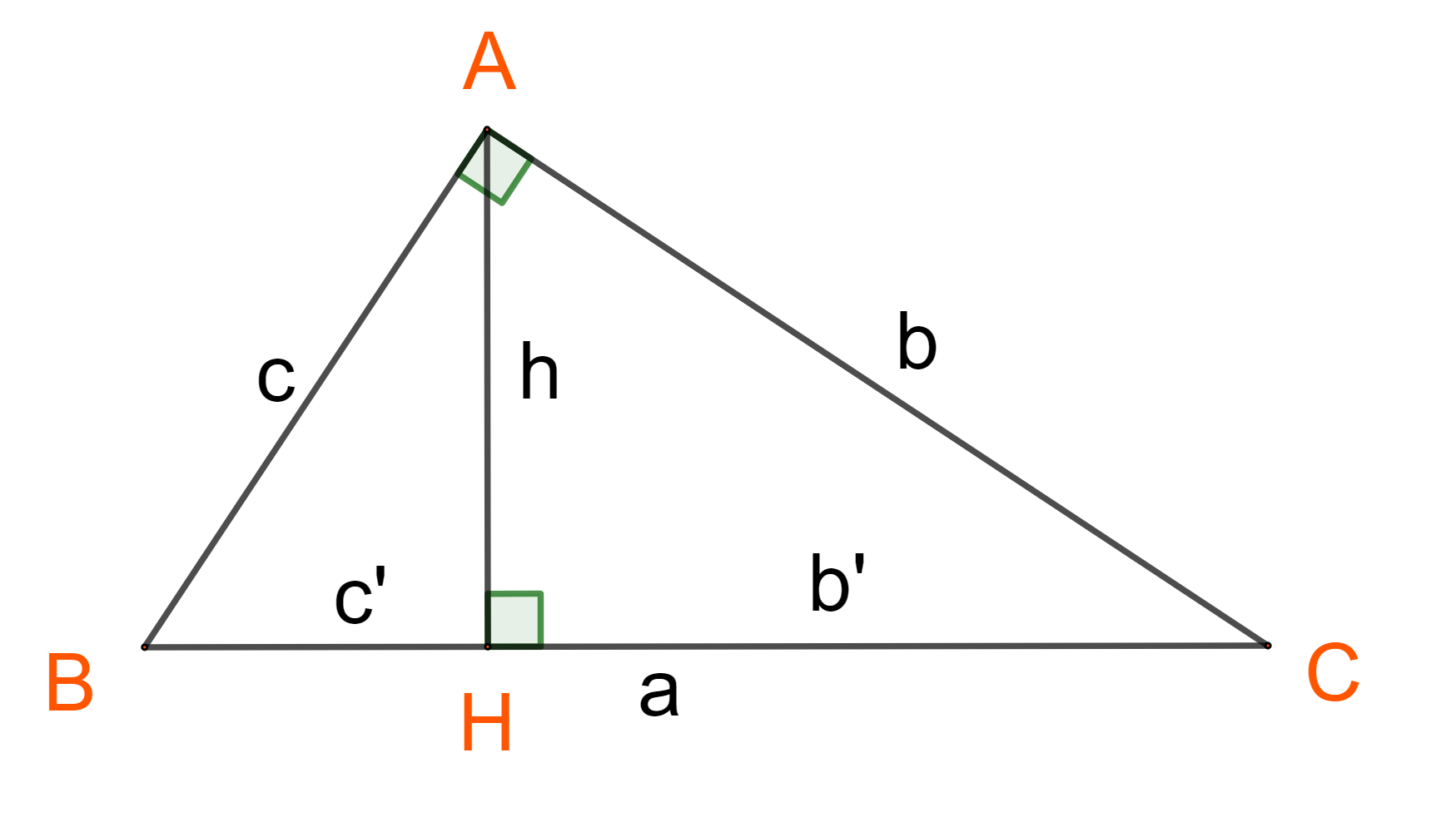
Hệ thức lượng tam giác vuông là tập hợp các công thức và định lý được sử dụng để tính toán các cạnh, góc và các yếu tố khác trong tam giác vuông. Dưới đây là các hệ thức lượng cơ bản trong tam giác vuông:

Những hệ thức lượng này giúp giải quyết các bài toán về tam giác vuông một cách hiệu quả, từ việc tính toán các cạnh và góc cho đến việc xác định diện tích và các yếu tố khác.

2.Hệ thức lượng trong tam giác vuông áp dụng cho các bài toán dạng nào

Hệ thức lượng tam giác vuông có thể được áp dụng để giải quyết nhiều loại bài toán trong hình học và lượng giác. Dưới đây là một số dạng bài toán phổ biến mà bạn có thể gặp:

Tính toán các cạnh hoặc góc khi biết một số thông số:

Khi biết hai cạnh: Sử dụng định lý Pythagoras để tính cạnh còn lại, hoặc sử dụng các hàm lượng giác (sin, cos, tan) để tính góc hoặc các cạnh khác.
Khi biết một góc và một cạnh: Sử dụng các công thức lượng giác để tính các cạnh còn lại và góc còn lại. Ví dụ, nếu bạn biết góc và cạnh kề, bạn có thể tính cạnh huyền bằng c=b / cos⁡(θ).

Tính diện tích của tam giác vuông:

Sử dụng công thức: Diện tích=1/2⋅a⋅b Trong đó a và b là hai cạnh góc vuông.

Giải các bài toán về đường cao trong tam giác vuông:

Tính chiều dài đường cao: Sử dụng công thức h^2 = p⋅q để tìm đường cao từ góc vuông đến cạnh huyền nếu biết các đoạn p và q mà đường cao chia cạnh huyền.
Tính độ dài các đoạn trên cạnh huyền: Sử dụng các hệ thức liên quan để tìm các đoạn bị chia bởi đường cao.

Xác định các yếu tố lượng giác:

Tính sin, cos, tan của các góc: Sử dụng các công thức lượng giác để tìm giá trị của các hàm lượng giác dựa trên thông tin về các cạnh hoặc góc trong tam giác vuông.

Giải các bài toán thực tế liên quan đến tam giác vuông:

Bài toán về khoảng cách và độ cao: Ví dụ, tính khoảng cách giữa các điểm trên mặt đất khi biết chiều cao của một vật và góc nhìn từ một điểm.
Bài toán về mô hình và thiết kế: Áp dụng các hệ thức lượng tam giác vuông để thiết kế và xây dựng các cấu trúc.

Xác định góc trong các bài toán hình học:

Tính góc khi biết tỷ số của các cạnh: Sử dụng công thức lượng giác để tìm các góc của tam giác vuông nếu biết tỷ số các cạnh.

Giải bài toán về độ dài của đoạn thẳng trong tam giác vuông:

Tính các đoạn thẳng phụ thuộc vào các góc và cạnh đã cho: Ví dụ, tính chiều dài của đoạn thẳng nối hai điểm trong một tam giác vuông.

Những ứng dụng này cho phép bạn giải quyết nhiều loại bài toán hình học và thực tế bằng cách sử dụng hệ thức lượng tam giác vuông một cách hiệu quả.

>> Tham khảo: Mệnh thủy hợp màu gì

3.Định lý tổng quát về tam giác vuông?

Trong tam giác vuông, có một số định lý tổng quát và quan trọng mà bạn nên biết:

Định lý Pythagoras:

Mô tả: Trong một tam giác vuông, bình phương của cạnh huyền (cạnh đối diện với góc vuông) bằng tổng bình phương của hai cạnh góc vuông.
Công thức: a^2 + b^2 = c^2 Trong đó c là cạnh huyền, và a và b là hai cạnh góc vuông.

Định lý tổng các góc trong tam giác vuông:

Mô tả: Tổng các góc trong một tam giác vuông luôn bằng 180 độ. Trong đó, một góc là 90 độ (góc vuông), và hai góc còn lại là các góc nhọn có tổng bằng 90 độ.
Công thức: Góc A+Góc B=90∘ (vì góc C = 90^\circ)

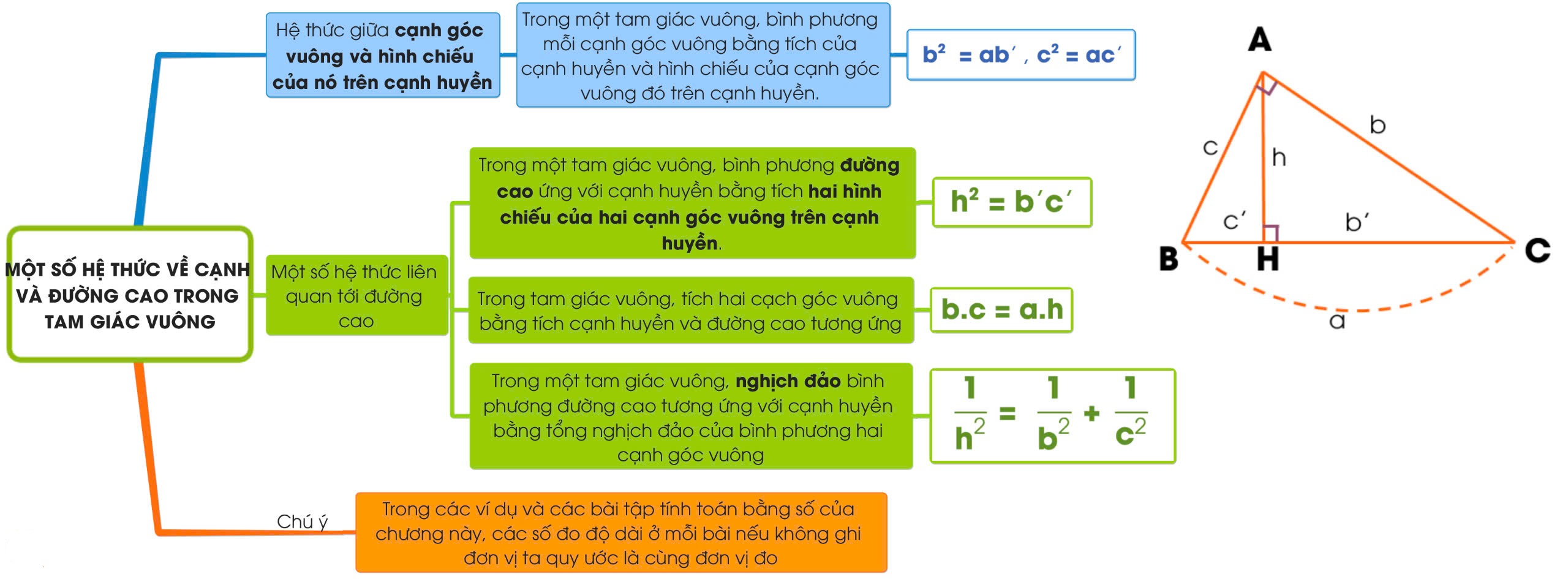
Định lý đường cao trong tam giác vuông:

Mô tả: Đường cao từ góc vuông đến cạnh huyền chia tam giác vuông thành hai tam giác vuông nhỏ hơn, và các tam giác này đều đồng dạng với tam giác vuông ban đầu và với nhau.

Công thức: h^2 = p⋅q Trong đó h là độ dài của đường cao từ góc vuông đến cạnh huyền, và p và q là các đoạn trên cạnh huyền mà đường cao chia ra.

Định lý về các đoạn chia cạnh huyền:

Mô tả: Đoạn cao chia cạnh huyền thành hai đoạn p và q. Nếu đường cao chia cạnh huyền thành hai đoạn, thì các đoạn này có quan hệ như sau: a2/p=b2/q=h2 Trong đó, a và b là các cạnh góc vuông, p và q là các đoạn trên cạnh huyền, và h là độ dài đường cao.

Định lý tương ứng giữa các góc và cạnh trong tam giác vuông:

Mô tả: Trong tam giác vuông, các tỷ số của các cạnh so với nhau liên quan đến các góc của tam giác thông qua các hàm lượng giác: sin⁡(θ)=cạnh đối / cạnh huyền cos⁡(θ)=cạnh kề / cạnh huyền tan⁡(θ)=cạnh đối / cạnh kề

Định lý về các tam giác vuông đồng dạng:

Mô tả: Trong tam giác vuông, các tam giác vuông nhỏ hơn mà được tạo thành bởi đường cao và các đoạn chia cạnh huyền đều đồng dạng với nhau và với tam giác vuông ban đầu.
Kết quả: Các tỷ lệ của các cạnh tương ứng giữa các tam giác vuông đồng dạng là giống nhau.

Những định lý này không chỉ cung cấp cơ sở để giải quyết các bài toán hình học trong tam giác vuông, mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực khác như vật lý, kỹ thuật, và nhiều lĩnh vực thực tiễn khác.

4.Hệ thức lượng trong tam giác vuông áp dụng thực tế như thế nào

Hệ thức lượng tam giác vuông có nhiều ứng dụng thực tế trong đời sống và các lĩnh vực khoa học kỹ thuật. Dưới đây là một số ví dụ về cách áp dụng hệ thức lượng tam giác vuông trong các tình huống thực tế:

Xác định khoảng cách

Ví dụ: Bạn đứng dưới chân một tòa nhà và muốn biết chiều cao của tòa nhà. Nếu bạn biết khoảng cách từ vị trí của bạn đến chân tòa nhà và góc nhìn từ điểm của bạn lên đỉnh tòa nhà, bạn có thể sử dụng công thức lượng giác để tính chiều cao của tòa nhà.
Công thức: Chiều cao = khoảng cách x tan (góc)

Thiết kế và xây dựng

Ví dụ: Trong xây dựng, khi thiết kế mái nhà, thang máy, hoặc các cấu trúc khác, các kỹ sư sử dụng hệ thức lượng để tính toán góc nghiêng, chiều dài của các đường chéo, và các kích thước khác để đảm bảo tính chính xác và độ ổn định của công trình.
Công thức: Sử dụng định lý Pythagoras để tính toán các kích thước cần thiết.

Đo đạc và bản đồ

Ví dụ: Trong công tác đo đạc, các nhà đo đạc viên sử dụng hệ thức lượng để tính toán khoảng cách giữa các điểm, đặc biệt khi không thể đo trực tiếp. Họ có thể sử dụng các góc và đoạn thẳng đã đo để tính các khoảng cách khác.
Công thức: Sử dụng các hàm lượng giác (sin, cos, tan) để tính toán các khoảng cách.

Điều chỉnh và thiết lập thiết bị

Ví dụ: Khi lắp đặt các thiết bị như ăng-ten, máy quay, hoặc các thiết bị cần được căn chỉnh chính xác, các kỹ sư sử dụng hệ thức lượng để đảm bảo thiết bị được đặt ở góc chính xác hoặc ở đúng vị trí.
Công thức: Sử dụng các công thức liên quan đến góc và chiều dài để tính toán các vị trí cần thiết.

Giải quyết vấn đề trong giao thông

Ví dụ: Trong việc thiết kế và phân tích các đường cong, góc cua, và các điểm giao nhau, các kỹ sư giao thông sử dụng hệ thức lượng để đảm bảo rằng các yếu tố này hoạt động hiệu quả và an toàn.
Công thức: Áp dụng các công thức lượng giác để tính toán các góc cua và các đoạn đường.

Ứng dụng trong vật lý

Ví dụ: Trong vật lý, các bài toán về chuyển động, độ nghiêng của mặt phẳng, và lực tác dụng có thể được giải quyết bằng cách sử dụng các hệ thức lượng tam giác vuông.
Công thức: Sử dụng các hàm lượng giác để tính toán các thành phần của lực và chuyển động.

Thiết kế đồ họa và mô hình 3D

Ví dụ: Trong thiết kế đồ họa và lập trình mô hình 3D, các nhà thiết kế sử dụng hệ thức lượng để tính toán các vị trí, khoảng cách, và góc trong không gian ba chiều.
Công thức: Sử dụng định lý Pythagoras và các hàm lượng giác để xác định các tọa độ và góc trong mô hình 3D.

Những ứng dụng này cho thấy hệ thức lượng tam giác vuông không chỉ là lý thuyết toán học mà còn là công cụ quan trọng để giải quyết các vấn đề thực tế trong nhiều lĩnh vực khác nhau.

Trên đây là các thông tin tổng quan được chúng tôi tổng hợp lại về hệ thức lượng tam giác vuông. Hy vọng rằng qua những thông tin hữu ích trên có thể giúp bạn trong quá trình học bài và làm bài tập nhé.

Nếu cần tư vấn màu sơn và loại sơn phù hợp với công trình của bạn, hãy liên hệ với chúng tôi:

CÔNG TY TNHH THƯƠNG MẠI ĐẦU TƯ SƠN PACIFIC

Hotline/Zalo: 0865663918

Địa chỉ Showroom 1: 269 Vườn Lài, P. Phú Thọ Hòa, Q.Tân Phú, TP.HCM

Địa chỉ Showroom 2: 243 Tô Ký, Ấp Mới, Trung Chánh, Hóc Môn, TP.HCM

Website: https://sonthaibinhduong.com/