Tìm hiểu công thức tính chu vi hình tròn nhanh nhất.

Mục Lục

Công thức tính chu vi hình tròn

1.Giới thiệu về chu vi hình tròn

Chu vi hình tròn là độ dài của đường viền hoặc biên giới của hình tròn. Nó có thể được tưởng tượng là khoảng cách xung quanh một chiếc bánh pizza tròn, hoặc là chiều dài của một sợi dây quấn quanh một vòng tròn. Chu vi của hình tròn là một trong những khái niệm cơ bản trong hình học và có ứng dụng rộng rãi trong toán học, kỹ thuật, vật lý, và đời sống hàng ngày.

Đặc Điểm Của Chu Vi Hình Tròn

Chu vi là một phép đo chiều dài, chỉ cho biết độ dài của đường viền xung quanh hình tròn.
Nó không thay đổi bất kể kích thước của hình tròn lớn hay nhỏ, miễn là bán kính (hoặc đường kính) thay đổi.

Như vậy, chu vi hình tròn là một khái niệm đơn giản nhưng rất quan trọng, giúp chúng ta hiểu và tính toán các đặc điểm của các hình tròn trong các tình huống thực tế.

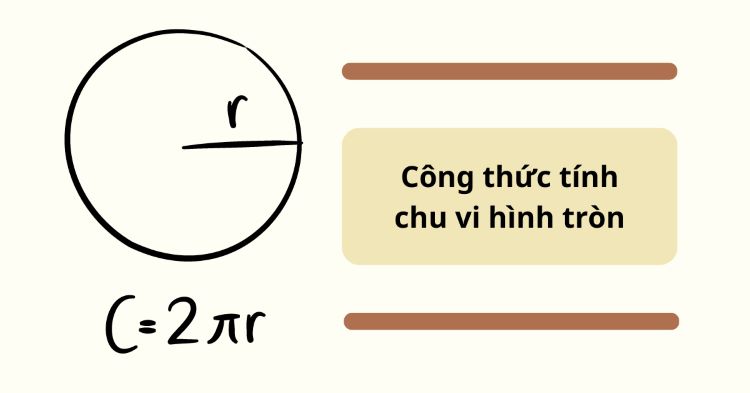
2.Công thức tính chu vi hình tròn

Công thức tính chu vi của hình tròn được tính bằng:

C=2πr

Trong đó:

C là chu vi (đơn vị đo là đơn vị của bán kính, ví dụ: mét, cm, km).
π là hằng số pi, có giá trị xấp xỉ 3.14159.
r là bán kính của hình tròn (tức là khoảng cách từ tâm hình tròn đến bất kỳ điểm nào trên đường tròn).

Ý nghĩa của Các Thành Phần trong Công Thức

Bán kính (r): Bán kính của hình tròn là khoảng cách từ tâm của hình tròn đến bất kỳ điểm nào trên đường viền của nó. Đây là một đại lượng quan trọng vì nó liên quan trực tiếp đến các đặc tính hình học khác của hình tròn.
Hằng số π: Đây là một hằng số toán học đặc biệt, biểu thị tỷ lệ giữa chu vi và đường kính của bất kỳ hình tròn nào. π\piπ là một số vô tỷ, có nghĩa là nó không thể biểu diễn chính xác bằng một số hữu tỷ và dãy số thập phân của nó vô hạn.

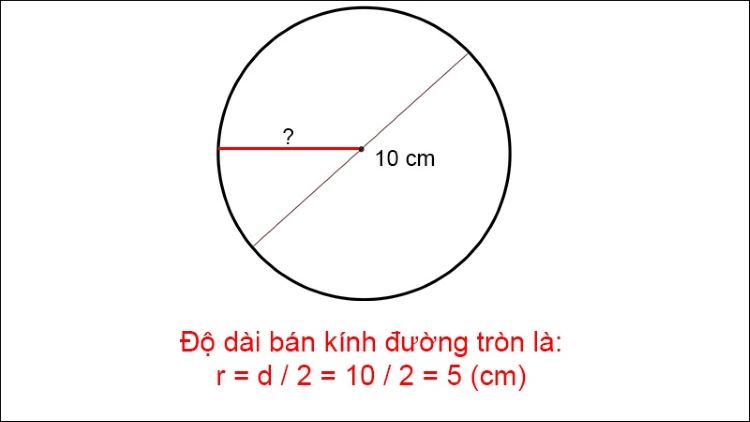
Liên Hệ với Đường Kính

Một cách khác để tính chu vi hình tròn là dựa trên đường kính (d), chính là hai lần bán kính:

C=πd

Vì đường kính ddd gấp đôi bán kính rrr (tức là d=2r), nên công thức này là một phiên bản khác của công thức chu vi.

3.Một số bài tập Công thức tính chu vi hình tròn

Dưới đây là một số bài tập về công thức tính chu vi của hình tròn, giúp bạn luyện tập và củng cố kiến thức:

Bài Tập 1:

Đề bài: Tính chu vi của một hình tròn có bán kính là 7 cm.

Hướng dẫn:
Áp dụng công thức tính chu vi:

C=2πr

Với r=7 cm, ta có:

C=2×3.14159×7≈43.9823 cm

Kết quả:
Chu vi hình tròn là khoảng 43.98 cm.

Bài Tập 2:

Đề bài: Một hình tròn có đường kính là 14 m. Tính chu vi của hình tròn đó.

Hướng dẫn:
Áp dụng công thức tính chu vi khi biết đường kính:

C=πd

Với d=14 m, ta có:

C=3.14159×14≈43.9823 m

Kết quả:
Chu vi hình tròn là khoảng 43.98 m.

Bài Tập 3:

Đề bài: Một chiếc bánh pizza có bán kính là 25 cm. Tính chu vi của chiếc bánh.

Hướng dẫn:
Áp dụng công thức tính chu vi:

C=2πr

Với r=25 cm, ta có:

C=2×3.14159×25≈157.0795 cm

Kết quả:
Chu vi của chiếc bánh pizza là khoảng 157.08 cm.

Bài Tập 4:

Đề bài: Tính chu vi của một hình tròn có bán kính 3.6 m.

Hướng dẫn:
Áp dụng công thức tính chu vi:

C=2πr

Với r=3.6 m, ta có:

C=2×3.14159×3.6≈22.619 m

Kết quả:
Chu vi của hình tròn là khoảng 22.62 m.

Bài Tập 5:

Đề bài: Một chiếc đồng hồ có mặt tròn với đường kính là 40 cm. Tính chu vi của mặt đồng hồ.

Hướng dẫn:
Áp dụng công thức tính chu vi khi biết đường kính:

C=πd

Với d=40 cm, ta có:

C=3.14159×40≈125.6637 cm

Kết quả:
Chu vi mặt đồng hồ là khoảng 125.66 cm.

Bài Tập 6:

Đề bài: Một sân vận động có hình tròn, bán kính của nó là 120 m. Tính chu vi của sân vận động.

Hướng dẫn:
Áp dụng công thức tính chu vi:

C=2πr

Với r=120 m, ta có:

C=2×3.14159×120≈753.982 m

Kết quả:
Chu vi của sân vận động là khoảng 753.98 m.

Những bài tập này giúp bạn làm quen với việc áp dụng công thức tính chu vi của hình tròn trong các tình huống thực tế.

4.Ứng dụng Công thức tính chu vi hình tròn

Chu vi hình tròn có rất nhiều ứng dụng trong thực tế, đặc biệt là trong các lĩnh vực toán học, kỹ thuật, xây dựng, vật lý và đời sống hàng ngày. Dưới đây là một số ứng dụng phổ biến của chu vi hình tròn:

Xây dựng và Kiến trúc

Thiết kế vòng tròn trong các công trình: Các công trình như bể chứa nước, các khu vực quay tròn, hoặc các cột trụ đều liên quan đến việc tính chu vi của hình tròn. Ví dụ, khi xây dựng một hồ bơi tròn hoặc một con đường vòng tròn, bạn cần tính chu vi để xác định lượng vật liệu cần thiết.
Đường kính và chu vi cột trụ: Trong thiết kế các cột trụ, chu vi được tính để xác định diện tích bề mặt hoặc tính toán vật liệu xây dựng.

Kỹ Thuật và Cơ Khí

Các bộ phận quay tròn: Trong các hệ thống cơ khí như động cơ, bánh răng, hoặc các bộ phận quay tròn khác, chu vi của hình tròn được tính để thiết kế các bộ phận sao cho chúng hoạt động hiệu quả.
Ống dẫn và đường ống: Chu vi được sử dụng để tính toán chiều dài của ống hoặc dây cáp có dạng hình tròn, từ đó xác định kích thước ống hoặc chiều dài vật liệu cần thiết.

Vật Lý

Chuyển động tròn đều: Chu vi hình tròn là một yếu tố quan trọng trong việc tính toán các chuyển động tròn đều, ví dụ như chuyển động của các hành tinh xung quanh Mặt Trời, hoặc trong các thiết bị cơ học quay.
Vật lý trong máy móc quay: Các máy móc như bàn xoay, bánh xe, hoặc các bộ phận trong tàu vũ trụ sử dụng chu vi để tính toán vận tốc hoặc chuyển động quay.

Thể Thao

Sân bóng đá và các môn thể thao khác: Trong nhiều môn thể thao, như bóng đá hoặc đua xe, việc tính toán chu vi của sân hoặc đường đua là rất quan trọng để xác định kích thước và các thông số kỹ thuật khác.
Đường đua: Chu vi của đường đua trong các môn thể thao như đua xe đạp, đua xe, hoặc thậm chí là đua ngựa cần phải được tính để xác định chiều dài của cuộc đua.

Đời Sống Hàng Ngày

Bánh và các món ăn tròn: Trong nấu ăn, chẳng hạn như khi bạn làm bánh pizza hoặc bánh sinh nhật, bạn cần tính chu vi của bánh để đo lượng nguyên liệu hoặc xác định kích thước của các vật dụng hỗ trợ (như khay nướng).
Đo dây hoặc dây điện: Khi bạn cần quấn một sợi dây xung quanh một vật tròn như cây cột, bạn sẽ cần tính chu vi để xác định chiều dài của dây.

Lĩnh Vực Nông Nghiệp

Tính chu vi đất trồng: Trong nông nghiệp, nếu bạn trồng cây trong các khu vực tròn hoặc hình tròn (như vườn cây ăn quả), chu vi của khu vực này sẽ giúp xác định diện tích và lượng nước, phân bón cần thiết.
Vòng tròn chăn thả: Chu vi cũng giúp tính toán diện tích khu vực chăn thả cho gia súc hoặc các vật nuôi.

Tính Toán và Toán Học

Giải quyết các bài toán về hình học: Trong toán học, chu vi hình tròn là một yếu tố quan trọng để giải quyết các bài toán về diện tích, thể tích, hoặc những vấn đề hình học phức tạp khác. Chu vi cũng liên quan đến việc tính toán các tỷ lệ, chẳng hạn như tỷ lệ giữa diện tích và chu vi của một hình tròn.

Lập Kế Hoạch và Thiết Kế Hệ Thống

Thiết kế vòng tròn và đường tròn trong giao thông: Các vòng xuyến, hay còn gọi là vòng xoay, trong giao thông cũng cần tính toán chu vi để xác định diện tích cần thiết cho các làn đường và khoảng cách di chuyển.
Thiết kế các hệ thống làm mát: Trong một số hệ thống làm mát, như quạt tròn, chu vi của quạt ảnh hưởng đến hiệu quả của quá trình làm mát.

Chu vi hình tròn là một khái niệm đơn giản nhưng có ứng dụng rất rộng rãi trong nhiều lĩnh vực khác nhau. Từ các công trình xây dựng, kỹ thuật, vật lý, thể thao đến đời sống hàng ngày, chu vi hình tròn đóng vai trò quan trọng trong việc tính toán các yếu tố liên quan đến không gian, diện tích và chuyển động.

Bài viết trên chúng tôi đã giới thiệu công thức tính chu vi của hình tròn, một kiến thức cơ bản nhưng vô cùng quan trọng trong toán học và ứng dụng thực tế. Nếu bạn đang tìm kiếm sự tư vấn về màu sơn và loại sơn phù hợp cho công trình của mình, hãy liên hệ với sonthaibinhduong.com để được hỗ trợ và lựa chọn sản phẩm tốt nhất cho dự án của bạn.

CÔNG TY TNHH THƯƠNG MẠI ĐẦU TƯ SƠN PACIFIC

Hotline/Zalo: 0865663918

Địa chỉ Showroom 1: 269 Vườn Lài, P. Phú Thọ Hòa, Q.Tân Phú, TP.HCM

Địa chỉ Showroom 2: 243 Tô Ký, Ấp Mới, Trung Chánh, Hóc Môn, TP.HCM

Website: https://sonthaibinhduong.com/